Нужно само решение!
1. Розв'яжіть нерівність sinx >0 :
Відповідь: (2πn; π+2πn), n∊Z
2. cosx >-1/2
Відповідь: (-2π/3+2πn;2π/3+2πn), n∊Z
3. tgx<√3
Відповідь: (-π/2 +πn; π/3+πn)
4. sin2(x) < 1/2 (застосуйте формулу пониження степеня)
Відповідь: (-π/4+πn;π/4+πn), n∊Z
5. 2 sin(x/2 - π/4) ≥ -1
Відповідь: [π/6 + 4πn;17π/6 + 4πn], n∊Z
6. 4sin(x/2)cos(x/2)≤ -1
Відповідь: [-5π/6+2πn;-π/6+2πn], n∊Z
7. sin3xcosx-cos3xsinx ≤ 1/2 (застосуйте формули додавання для тригонометричних функцій)
Відповідь: [-7π/12 + πn;π/12 + πn], n∊Z
X=-2
Объяснение:
Сперва приводим оба уравнение к виду y=kx-b
Получаем два уравнения
y=-3x+1
y=-x+5
Дальше,
Чтобы нарисовать прямую нужно найти всего две точки и соединить их.
Подставим x=0 в первое уравнение получим y=1 вот и наша первая точка (0;1)
Подставим x=1 получим y=-2
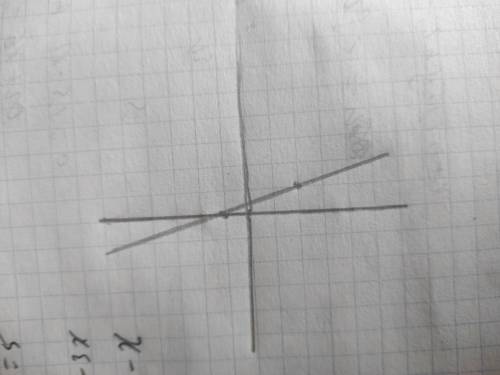
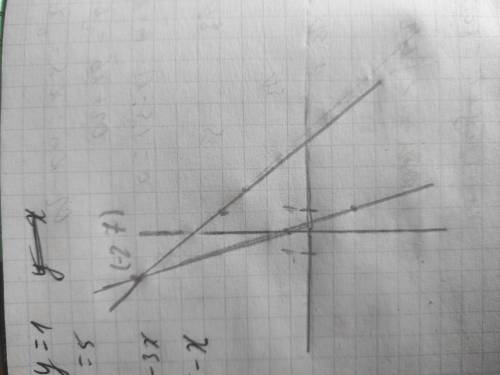
Вторая точка (1;-2) есть, можно строить первую прямую(есть фотография)
Строим второй график по такому же принципу
X=1 y=4(подставлять можно какие угодно x=a точки лишь бы было удобно рисовать)
X =2 y=3
Рисуем две прямые и смотрим на пересечение на графике.
В итоге получаем точку пересечения (-2;7)
-2x - 4 > 0
-2x > 4
2x < -4
x < -2
x∈(-∞; -2)