Простыми преобразованиями эту задачу не решить, будем использовать арифметику остатков.
1-ое свойство, которое понадобится
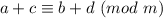
То есть мы спокойно можем заменить каждое слагаемое сравнимым с ним по модулю m. То есть каждое слагаемое в нашей сумме будем рассматривать отдельно.
2-ое свойство, которое нам понадобится:
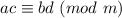
То есть довольно аналогичная вещь в произведении
На нашем примере все увидим
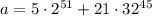
Находим остатки по модулю 31
Рассматриваем первое слагаемое. Просто двойка не годится, нам нужно найти ближайшее к 31 число, превосходящее его (иногда там в отрицательные числа залезаем, например,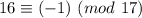 
, но сейчас это не нужно), нам повезло, это 32
Учитываем, что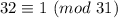 
, получаем
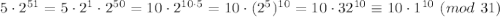
То есть остаток от деления первого слагаемое на 31 получился равным 10. Прекрасно, аналогично со вторым
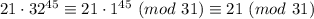
Остаток 21, чудесно. Выполняем последний шаг.
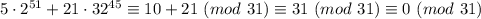
То есть остаток от деления исходного числа на 31 равен 0, следовательно, исходное число делится на 31, что и требовалось доказать.
1.найдите 25-ый член арифметической прогрессии -3 -6 d=-6+3=-3
a25=a1+24d=-3-72=-75
2.найдите 10 -й член арифметической прогрессии 3 7 d=7-3=4
a10=a1+9d=3+36=39
3.сумма первых шести членов арифметической прогрессии равна 9 разность между четвертым и вторым членами 0.4 найдите первый член прогрессии.
a4-a2=0.4 a1+3d-a1-d=0.4 2d=0.4 d=0.2
S6={2a1+5d}/2*6 {2a1+1}*3=9 2a1+1=3 2a1=2 a1=1
4. сумма трех чисел образующих арифметическую прогрессию равна 111 второе число больше первого в 5 раз. найдите эти числа
a1+a1+d+a1+2d=111 3a1+3d=111 a1+d=37
a1+d=5a1 5a1=37 a1=7.4 a3=111-(7.4+37)=66.6
7.4 37 66.6
5. найдите разность арифметической прогрессии если а21=15 а1=5
a21=a1+20d 20d=15-5=10 d=0.5
6. найдите сумму всех натуральных чисел от 2 до 102 включительною
n=102-2+1=101 S101=(2*2+100*1)/2*101=52*101=5252
8. найдите сумму бесконечно убывающей геометрической прогрессии если б1=2 q=0.875
S=b1/1-q=2/(1-0.875)=2/0.125=2000/125=16
9. найдите сумму бесконечно убывающей геометрической прогрессии 9 -3 1
q=-1/3
S=9/(1+1/3)=9/(4/3)=9*3/4=27/4=6.75
