1) 2x² - xy = x(2x - y)
2) ab + 3ab² = ab(1 + 3b)
3) 2y⁴ + 6y³ - 4y² = 2y²(y² + 3y - 2)
4) 2a(a - 1) + 3(a - 1) = (a - 1)(2a + 3)
5) 4x - 4y + ax - ay = (4x - 4y) + (ax - ay) = 4(x - y) + a(x - y) = (x - y)(4 + a)
1) 2a²b² - 6ab³ + 2a³b = 2ab(ab - 3b² + a²)
2) a²(a - 2) - a(a - 2)² = a(a - 2)(a - a + 2) = 2a(a - 2)
3) 3x - xy - 3y + y² = (3x - xy) - (3y - y²) = x(3 - y) - y(3 - y) = (3 - y)(x - y)
4) ax - ay + cy - cx + x - y = (ax - ay) - (cx - cy) + (x - y) =
= a(x - y) - c(x - y) + (x - y) = (x - y)(a - c + 1)
3.
xy - x² - 2y + 2x = (xy - x²) - (2y - 2x) = x(y - x) - 2(y - x) = (y - x)(x - 2)
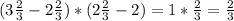
ответ: первый случай, A=60°, C=30°
Второй случай, C=60°,A=30°
Объяснение:
Для начала нарисуем прямоугольный треугольник ABC. Позже нарисуем внешний угол к углу C,обозначим этот внешний угол, как ACD. По условию ACD=120, а так как внешние углы-это углы, смежные с каким-нибудь углом треугольника, то ACD+C=180 C=180-120=60°. Из теоремы суммы углов треугольника, угол A=180-60-90=30°.
Рассмотрим 2 случай:
Нарисуем снова прямоугольный треугольник ABC и нарисуем внешний угол к углу a, обозначим его, как BAD. По условию угол BAD=120°,а так как внешний угол- это угол, смежный с каким-нибудь углом в треугольнике, то угол A=60°,из теоремы суммы углов, угол C=180-90-60=30
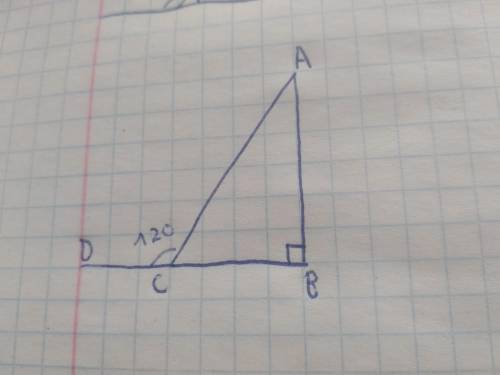
sin²α+2sinαcosα+cos²α=0,25
sin2α=2sinαcosα
2sinαcosα=0,25-(sin²α+cos²α)