Доказать тождество 1. 3-cos^2*a-sin^2*a=2 2. 1-sina*cosa*ctga=sin^2*a - id385458720200826 от Remka228 26.08.2020 20:11

Question

Алгебра: Доказать тождество 1. 3-cos^2*a-sin^2*a=2 2. 1-sina*cosa*ctga=sin^2*a

Remka228 · Accepted Answer

1. Напишите уравнение касательной к кривой y=sqrt(2-5x) в точке ее пересечения с осью ординат.

Касательная задается уравнением:

y = f ’(x0) · (x − x0) + f (x0)

Здесь f ’(x0) — значение производной в точке x0, а f (x0) — значение самой функции.

В точке пересечения графика с осью ординат переменная х равна 0.

f(x=0) = √2.

f'(x) = (-5/(2√(2-5x))), f'(x=0) = -5/(2√2)

Тогда уравнение касательной в точке х = 0 имеет вид:

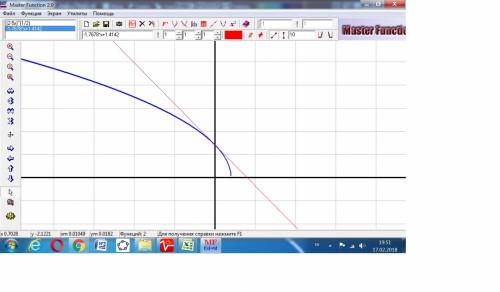
у(кас) = (-5/(2√2))*х + √2 или с приближёнными значениями:

у(кас) = -1,76777х + 1,414214.

Доказать тождество 1. 3-cos^2a-sin^2a=2 2. 1-sinacosactga=sin^2*a