ВведениеПособие содержит подробные разработки уроков по техноло-гии, которые будут полезны учителям, работающим по учебному комплекту под редакцией В.Д. Симоненко (М.: Вентана-Граф). Курс рассчитан на два часа в неделю (продолжительность каж-дого урока – два часа), 68 часов в год. Этапы некоторых уроков представлены в вариантах; учитель может выбирать вид урока в зависимости от материально-технической базы мастерских, уровня первоначальных знаний и умений учащихся. Особенно-стью данных поурочных разработок является наличие переходного этапа – от повторения пройденного к изучению нового материала; на этом этапе учитель формулирует проблему, над которой класс будет работать в течение урока.
Объяснение:
1.Область определения D(x) - Х∈(-∞;+∞) - непрерывная. Вертикальных асимптот - нет
2. Пересечение с осью Х. Решаем квадратное уравнение: Y=0
при х1,2 = - 1/3.
3. Пересечение с осью У. У(0) = 1.
4. Поведение на бесконечности.limY(-∞) = + ∞ limY(+∞) = +∞ - горизонтальных асимптот - нет.
5. Исследование на чётность.Y(-x) = 9*x² - 6*x+1 ≠ Y(x).
Функция ни чётная ни нечётная.
6. Производная функции.Y'(x)= 18*x -6 = 0.
Корень Х= -1/3.
7. Локальные экстремумы. Минимум – Ymin(- 1/3) =0.
8. Интервалы возрастания и убывания. Возрастает - Х∈(-1/3;+∞),
убывает = Х∈(-∞;-1/3)
8. Вторая производная - Y"(x) = 18.
Корня производной - точка перегиба - нет.
9. Вогнутая – «ложка» Х∈(-∞;+∞).
10. Область значений Е(у) У∈(0;+∞)
11. Наклонная асимптота -. Уравнение: lim(oo)(k*x+b – f(x).
k=lim(∞)(9x+6+1)= ∞ - наклонных асимптот - нет
12. График в приложении.
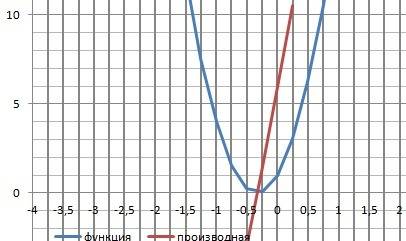
Объяснение:
решение представлено на фото