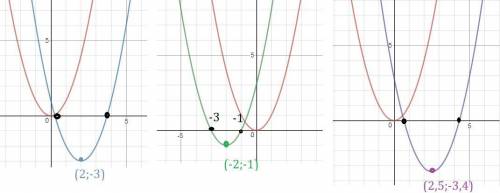
1) Шаблон y=x²
Вершина в точке (2;-3)
Нули функции
(x-2)²-3=0 ⇒
(x-2)²=3
x-2= -√3 или х-2=√3
х=2-√3 или х=2+√3
2) Шаблон y=x²
Вершина в точке (-2;-1)
Нули функции
(x+2)²-1=0 ⇒
(x+2)²=1
x+2= -1 или х+2=1
х=-3 или х=-1
3) Шаблон y=x²
Вершина в точке (2,5;-3,4)
Нули функции
(x-2,5)²-3,4=0 ⇒
(x-2,5)²=3,4
x-2,5= -√3,4 или x-2,5=√3,4
х= 2,5 -√3,4 или х=2,5 +√3,4
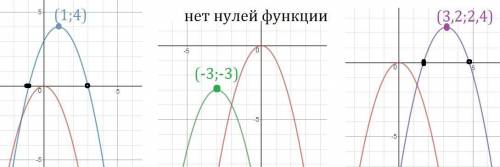
4)Шаблон y= - x²
Вершина в точке (1;4)
Нули функции
-(x-1)²+4=0 ⇒
(x-1)²=4
x-1= -2 или x-1=2
х= -1 или х=3
5)Шаблон y= - x²
Вершина в точке (-3;-3)
Нули функции
-(x+3)²-3=0 ⇒
(x+3)²=-3
уравнение не имеет корней.
Парабола не пересекает ось Ох
6)Шаблон y= - x²
Вершина в точке (3,2;2,4)
Нули функции
-(x-3,2)²+2,4=0 ⇒
(x-3,2)²=2,4
x-3,2= - √2,4 или x-3,2= √2,4
x= 3,2 - √2,4 или x = 3,2+ √2,4
y=-x^2 Это квадртичная функция
График функции- парабола , ветви направлены вниз, т.к. а меньше нуля.
Это самая простая квадратичная функция (-х)^2 =х^2 (четная степень), значит функция чётная.
У параболы всегда есть вершина.Здесь это А(0;0).Наша парабола касается оси абсцисс в точке А(0;0), проходя через начало координат.
Любая парабола имеет ось симметрии. У нас это прямая х=0(ось ординат)
Чтобы построить график этой функции надо найти координаты точек
У(0)=0 У(-1)=-1
У(1)=-1 У(-2)=-4
У(2)=-4 У(-3)=-9
У(3)=-9
Можно в табличке записать
Х 0 1 2 3 4 -1 -2 -3
У 0 -1 -4 -9 -16 -1 -4 -9
Построй систему координат, а потом по точкам нарисуешь плавно параболу, только не заканчивай ветви на точках, ветви идут в бесконечность, т.к. Х может быть любым. Желаю удачи.
4cos²x-2cosx-2=0
2cos²x-cosx-1=0
cosx=a
2a²-a-1=0
D=1+8=9
a1=(1-3)/4=-1/2⇒cosx=-1/2⇒x=+-2π/3+2πn
-2π≤-2π/3+2πn≤-π/2 U -2π≤2π/3+2πn≤-π/2
-4π/3≤2πn≤π/6 U -8π/3≤2πn≤-7π/6
-2/3≤n≤1/12 U -4/3≤n≤-7/12
n=0⇒x=-2π/3 U n=-1⇒x=-π/3
a2=(1+3)/4=1⇒cosx=1⇒x=2πn
-2π≤2πn≤-π/2
-1≤n≤-1/4
n=-1⇒x=-2π
ответx={-2π/3;-π/3;-2π}