{2х²-ху-у²-10х-8у-12=0
{2х²+3ху+у²+х-у-6=0
Найдем корни уравнений относительно у
1)2х²-ху-у²-10х-8у-12=0
-у²+(-х-8)у+(2х²-10х-12)=0 |:(-1)
у²+(х+8)у+(12+10х-2х²)=0
D = (x+8)²-4*1*(12+10х-2х²) = x²+16x+64-48-40x+8x² = 9x²-24x+16 = (3x-4)²
y12 =( -(x+8)±(3x+4))/2
y1=(-x-8+3x+4)/2 =(2x-4)/2 = x-2
y2 = (-x-8-3x-4)/2 = (-4x-12)/2 = -2x-6
2)2х²+3ху+у²+х-у-6=0
y²+(3x-1)y+(2x²+x-6) = 0
D = (3x-1)²-4*1*(2x²+x-6) = 9x²-6x+1-8x²-4x+24 = x²-10x+25 = (x-5)²
y12 =(-(3x-1)±(x-5))/2
y1 = (-3x+1+x-5)/2 = (-2x-4)/2 = -x-2
y2 = (-3x+1-x+5)/2 = (-4x+6)/2 = 3-2x
Теперь соединим все у в 4 системы:
а)
{y = x-2
{y= -x-2
Т.к. левые части равны => мы можем приравнять и правые
x-2 = -x-2
x+x = -2+2
2x = 0
x=0
Подставляем значение х для нахождения y
(можно подставить в любое уравнение данной системы,ответ будет одинаковый. То же правило и для последующих систем)
y = 0-2 = -2
б)
{y=x-2
{y=3-2x
x-2 = 3-2x
x+2x = 3+2
3x = 5
x=5/3
Подставляем значение х для нахождения y
y = 3-2*5/3= 3-10/3= (9-10)/3 = -1/3
в)
{y= -2x-6
{y= -x-2
-2x-6 = -x-2
-2x+x = -2+6
-x= 4
x= -4
Подставляем значение х для нахождения y
y = -2*(-4)-6 = 8-6 = 2
г)
{y= -2x-6
{y=3-2x
-2x-6 = 3-2x
-2x+2x = 3+6
0x=9
х∈ø
ответ: (0;-2) , (5/3;-1/3) , (-4;2)
Пусть число записано в виде произведения степеней простых множителей:
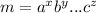, где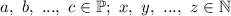 
Тогда, число делителей этого числа определяется по формуле:
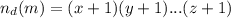
Рассмотрим некоторое число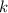 
. Пусть 
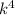имеет 85 делителей. Разложим число 85 на множители:
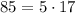
Заметим, что число 85 раскладывается на какие бы то ни было множители единственным образом.
Зная это, необходимо рассмотреть две ситуации.
1) Число делителей находилось как произведение из одного множителя (условное произведение):
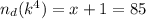
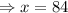
Тогда, число 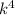имеет вид:
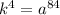
Найдем число :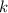
![k=\sqrt[4]{a^{84}}](/tpl/images/1399/3019/a4e5c.png)
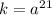
Найдем число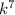 
:
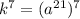
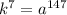
Число делителей этого числа:
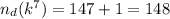
2) Число делителей находилось как произведение из двух множителей:
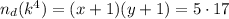
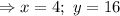
Тогда, число 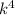имеет вид:
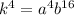
Найдем число :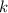
![k=\sqrt[4]{a^4b^{16}}](/tpl/images/1399/3019/39b3e.png)
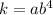
Найдем число :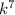
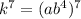
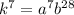
Число делителей этого числа:
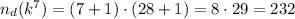
ответ: 148 или 232
подставляем это в первое: 3(-4y-4)-2y=16
-12y-12-2y=16
-14y=28
y=-2
подставляем значение y во второе: x= 8-4 = 4
ответ: (4; -2)