Сначала найдём значения параметра k. Приравняем оба графика, поскольку они пересекаются, а затем уже наложим дополнительные условия.
kx = -x² - 1
x² + kx + 1 = 0
Графики будут иметь одну общую точку тогда и только тогда, когда данное квадратное уравнение будет иметь 1 корень. Найдём те k, при которых данное квадратное уравнение имеет 1 корень. Если квадратное уравнение имеет 1 корень, то его дискриминант строго равен 0.
D = b² - 4ac = k² - 4
D = 0 k² - 4 = 0
k² = 4
k1 = 2; k2 = -2
Значит, при k = 2 и при k = -2 оба графика буцдут иметь ровно одну общую точку.
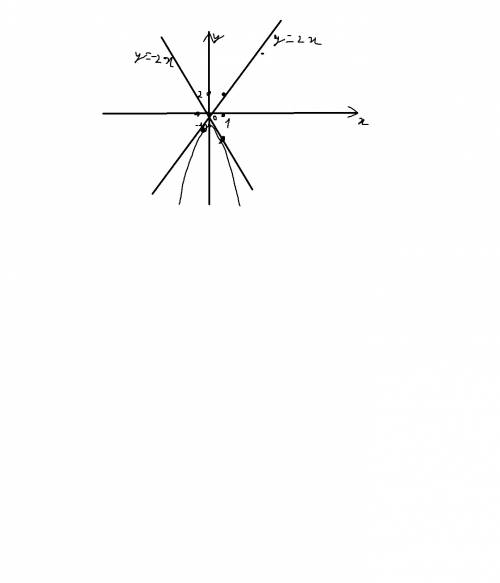
Теперь построим такие прямые. Надо построить y = -x² - 1 и прямые y = 2x, y = -2x. Скажу просто на всякий случай, что обе прямые будут симметричны относительно оси ox. Сейчас пришлю рисунок с построением(надеюсь, вы понимаете, как строятся эти прямые). Построение лишь приближённое и грубое, но видно, что обе прямые касаются параболы в какой-то точке, то есть фактически имеет с ней одну единственную точку.
18 дней и 36 дней
Объяснение:
х - скорость работы первой бригады
у - скорость работы второй бригады
Всю работу примем за 1.
По условию, работая вместе бригада выполнит работу за 12 дней, значит 1/(х+у)=12.
Первая бригада выполнит половину работу 1/(2х) и вторая работа выполнит оставшуюся часть, т.е. половину работы 1/(2у) за 27 дней.
Составим и решим систему уравнений:
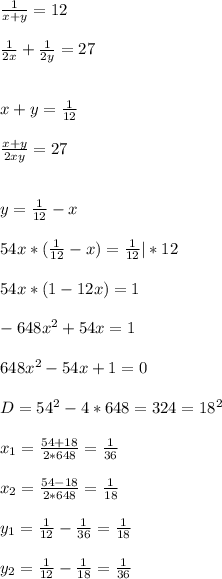
Т.е. скорость одной бригады 1/18, а скорость другой 1/36
1:1/18=18 дней потребуется одной бригаде на выполнение всей работы
1:1/36=36 дней потребуется другой бригаде для выполнения всей работы
s = v×t
Отсюда выразим время:
t = s : v (1)
Таким образом, мы находим время, за которое автомобиль путь s.
За это же время t мотоцикл со скоростью u пройдет путь равный:
s₂ = u×t
Вместо t подставляем выражение (1) и получаем:
s₂ = u × s : v - это путь, который пройдет мотоцикл за то же время, за которое автомобиль путь s.