Из 9 солдат нужно выбрать некоторых 7. Число сделать это равно числу сочетаний из 9 элементов по 7:
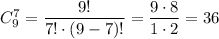
Из 6 сержантов нужно выбрать некоторых 4. Число сделать это равно числу сочетаний из 6 элементов по 4:
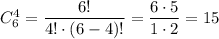
Из 4 офицеров нужно выбрать некоторого 1. Число сделать это равно числу сочетаний из 4 элементов по 1:
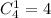
Так как выбор солдат, выбор сержантов и выбор офицера попарно независимы, то соответствующие нужны перемножить. То есть любому выбору солдат мы можем сопоставить любой выбор сержантов, а также любой выбор офицера.
Общее число вариантов:
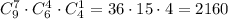
ответ: 2160 вариантов
1 этап: Составление математической модели.
Производительность ученика х деталей в час
из условия производительность мастера х+15 деталей в час
Мастер работал 6 час. значит изготовил 6*(х+15) деталей
Ученик работал 8 час. значит изготовил 8*х деталей
По условию мастер изготовил деталей в 3 раза больше
Таким образом 6*(х+15)=3*8*х
2 этап: Работа с составленной моделью
6(x+15)=24x | :6
(x+15)=4x
15=3x
x=5
3 этап: ответ на вопрос задачи.
За х мы обозначили производительность ученика и она равна 5 дет/час
значит производительность мастера 5+15=20 дет/час
Мы ответили на вопрос задачи.
Производительность мастера 20 дет/час
Расстояние между городами х,Не учитывая направления движения найдем среднуюю скорость при движении на участке b,Этот участок автобус проходит два раза.Vср=2b/(b/30+b/60)=2b/(3b/60)=40 км/чВсе тоже самое справедливо для участка с.Значит и там средняя скорость равна 40 км/ч.Ровные и неровные участки равны.Составляем уравнение, учитывая, что х-расстояние между городами проезжам два раза и делим на два участка. То есть изначально уравнение выглядит так:2x/(2*50)+2x/(2*40)=2.25x/50+x/40=2.250.02x+0.025x=2.250.045x=2.25 ,x=50Получается 50 км.