Вычислите:
1) sin 105° * sin 75°; 2) 4sin 37,5° * sin 7,5°; 3) 8sin 22,5° * cos 7,5°
1 ) sin 105° * sin 75° = (1/2)* (cos(105° -75°) - cos(105°+75°) )=
(1/2)* (cos30°-cos180°) =(1/2)* ( (√3)/ 2 - (-1) ) = (1/2)*((√3) / 2+ 1 ) = (√3+2)/4
- - - - - - -
2 ) 4sin 37,5° * sin 7,5° =2*(cos(37,5° - 7,5°) - cos(37,5° +7,5°) ) =
2*(cos30° - cos45°) =2*( (√3)/2 -(√2) /2) = √3 - √2 .
- - - - - - -
3 ) 8sin 22,5° * cos 7,5° = 4*( sin(22,5°+7,5°) +sin(22,5°-7,5°) ) =
4*( sin30° + sin15° ) = 4*( 1/2 + sin(60 - 45°) ) =
4*( 1/2 + sin60°*cos45°- cos60°*sin45° ) = || cos45°=sin45 =√2 / 2 ||
= 4*( 1/2 + √2 (√3 - 1) / 4 ) = 2 + √6 - √2 .
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
P.S. sin15° =sin(45° -30°) = sin45°*cos30° - cos45°* sin30° =
(√2 / 2)*(√3 / 2 -1 / 2) = (√6 - √2) / 4 .
sin15° =√( (1 -cos30°) / 2 ) =√( (1 -√3 /2) / 2 ) =√( (2-√3 ) / 4 ) =
√( (4-2√3 ) / 8 ) =√( (3-2√3+1) / 8 ) =√( (√3 - 1 )² / 8 ) = (√3 - 1) /2√2 =
√2(√3 - 1) /4 = (√6 - √2) / 4 .
48 квадратных сантиметров
Объяснение:
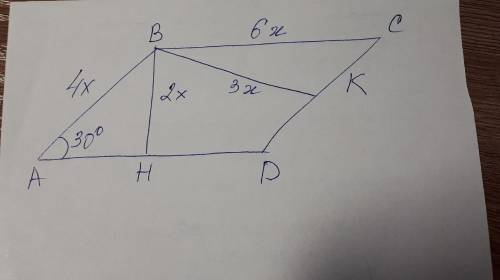
1) Примем одну высоту параллелограмма за 2х (на рисунке это сторона BH), тогда вторую высоту примем за 3х (на рисунке это сторона BK).
2) Поскольку катет против угла в 30° равен половине гипотенузы, то из треугольника АВН получаем, что гипотенуза АВ = 4х.
3) Далее рассмотрим треугольник ВСК. Получаем, что сторона ВС= 6х
4) Затем вычислим периметр параллелограмма: (4х+6х)*2=40 сантиметров
5) 20х=40, откуда х=2
6) Таким образом, можно сделать вывод, что одна сторона 4х=4·2=8 см.
7) Высота проведенная к этой стороне 3х=3·2=6 см
8) Таким образом получаем, что площадь параллелограмма равна 8*6=48 квадратных сантиметров