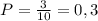
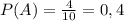
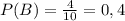
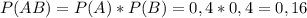
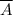 и найдём его вероятность.
и найдём его вероятность.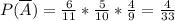
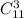 ). И вычислить число вариантов выбора 3 нарциссов из 6 (
). И вычислить число вариантов выбора 3 нарциссов из 6 ( ). А потом по классической формуле вероятности находится требуемая вероятность. Не всегда, но в данном случае такой путь боле громоздок.
). А потом по классической формуле вероятности находится требуемая вероятность. Не всегда, но в данном случае такой путь боле громоздок.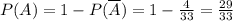
Данное уравнение не имеет целых корней.
Используем метод Феррари:
уравнение вида
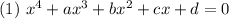
с замены 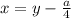
приводим к виду:
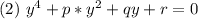
где:
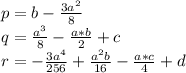
добавим и вычтем из левой части уравнения 2 выражение 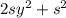 , где s - некоторое число:
, где s - некоторое число:

получим:
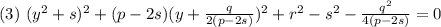
Пусть s - корень уравнения
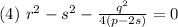
Тогда уравнение 3 примет вид:
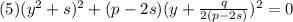
Избавляемся в уравнении 4 от знаменателя:
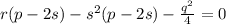
Раскроем скобки и получим:
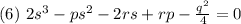
Уравнение 6 называется кубической резольвентой уравнения 4 степени.
Разложим уравнение 5 на множители:
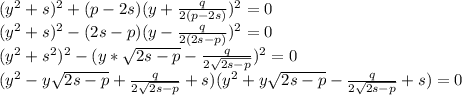
Получим два квадратных уравнения:
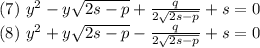
Применяем этот метод для решения уравнения
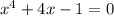
Перепишем уравнение в полном виде:
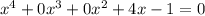
коэффиценты:
a=0
b=0
c=4
d=-1
определяем p,q и r:
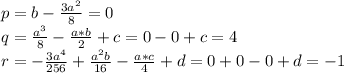
ищем s:
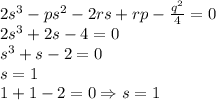
подставляем p,q,r и s в квадратные уравнения 7 и 8:
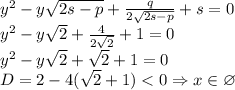
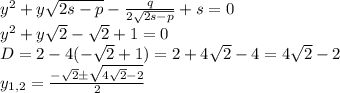
Теперь находим x:
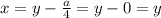
ответ: 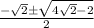
1.х(х+8)=0
х=0 или х=-8
ответ: 0;-8
2. у(у+30)=0
у=0 или у=-30
ответ: 0;-30