Відповідь:
Воспользуемся формулой
1) sin72°cos18°+sin18°cos72°
sin(а+b)=sin a*cos b+cos a* sin b
sin (72°+18°) = sin 90° = 1
2) cos81°cos21°+sin81°sin21°
3) cos15+cos75 = cos (15+75)= cos 90 = 0
4) sin 7 α - sin α = sin (7 α - α) = sin 6 α
5) cos 20 * cos 40
нужно умножить выражение на sin20, чтобы получился синус двойного угла, и тут же разделить это выражение. Думаю, если оставить все на словах, вы мало поймете, хорошо, запишу: cos20 * cos40 =1(2sin20*cos20)*cos40= 1*sin40*cos40*cos80/sin20
В общем, суть такая.
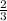от того, что осталось после первого деня, то после второго дня работы осталась 
от того, что осталось после первого дня работы. По условию, после двух дней работы осталось 2 банки, соответственно =2, из чего следует, что во второй день израсходовали 4 банки с краской (так как 2×2=4). По условию сказано, что в первый день израсходовали половину всех банок +1. Значит, 4 банки - это половина всех банок -1. Соответственно, половина - это 4+1=5. В первый день израсходовали 5+1=6 (банок с краской), во второй день израсходовали 4 (банки с краской), а осталось на третий день еще 2 (банки с краской). Суммируем все количество банок: 6+4+2=12.
2sin3x cos3x - cos3x=0
cos3x (2sin3x - 1)=0
cos3x =0
3x=π/2 + πn, n ∈ Z
x=π/6 + πn/3, n ∈ Z
2sin3x - 1 =0
sin 3x = 1/2
Б) 2sin²x + 3cosx + 3=0
2(1-cos²x)+3cosx + 3 =0
2 - 2cos²x + 3cosx + 3=0
-2cos²x + 3cosx +5 = 0
2cos²x - 3cosx - 5 = 0
Пусть cos x = t (|t|≤1), тогда получаем
2t²-3t-5=0
D=b²-4ac=9+4*5*2=49; √D=7
t1=(3+7)/4 = 2.5 - не удовлетворяет условие при |t|≤1
t2=(3-7)/4=-1
Обратная замена
cos x = -1
x=π + 2πn, n ∈ Z