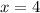
Объяснение:
Чтобы решить уравнение, нужно понять три вещи:
1. Основание логарифма должно быть всегда больше нуля, и никогда быть равной единице
2. Логарифм равен единице тогда и только тогда, когда аргумент равен основанию
3. Аргумент логарифма должен выражаться положительным числом
Таким образом, приходим к системе:
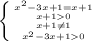
Сначала решим уравнение:
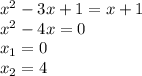
Первый корень x1 = 0 не удовлетворяет третьему условию, значит этот корень отбрасываем
Второй корень x2 = 4 удовлетворяет всем условиям данной системы, поэтому является единственным корнем
отметим точки -3 и 6 на координатной прямой и рассмотри значения выражения (x-6)(x+3) на трех промежутках:
(-∞;-3];
[-3;6];
[6;+∞).
выражение (x-6)(x+3) принимает значения
2)в неравенстве
1-x≠0
x≠1
далее на координатной прямой расставляем точки x=0 и
x=1 ВЫКОЛОТАЯ
далее аналогично получаем, что исходное выражение принимает отрицательные значения на ИНТЕРВАЛЕ(т.к. знак строгий) x∈(0,1)
3) на общей координатной прямой отмечаем два полученных нами ранее промежутка
x∈[-3;6] и
x∈(0,1)
и отбираем только те точки, которые принадлежат обоим промежуткам, а именно x∈(0;1)
ответ: (0;1)