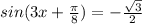
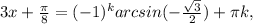 k∈Z
k∈Z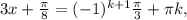 k∈Z
k∈Z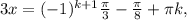 k∈Z
k∈Z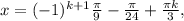 k∈Z
k∈Z
Відповідь:
Пояснення:
Щоб дослідити функцію на парність, необхідно перевірити, чи є вона симетричною відносно осі y (ось ординат). Функція f(x) = 3x⁵ - 2x⁷ має парність, якщо виконується умова f(x) = f(-x) для будь-якого значення x.
Давайте перевіримо цю умову, підставивши -x замість x у функцію і порівняємо результат з вихідним виразом:
f(-x) = 3(-x)⁵ - 2(-x)⁷
= -3x⁵ + 2x⁷
Ми бачимо, що f(-x) = -3x⁵ + 2x⁷ не дорівнює вихідному виразу f(x) = 3x⁵ - 2x⁷. Отже, функція f(x) = 3x⁵ - 2x⁷ не є парною (симетричною відносно осі y).
Ви маєте рацію. Я пропустив важливу частину. Якщо функція не є парною, тоді її можна віднести до одного з двох інших видів - непарної або загального виду.
Щоб перевірити, чи є функція непарною, необхідно перевірити, чи виконується умова f(x) = -f(-x) для будь-якого значення x.
Давайте застосуємо цю умову до функції f(x) = 3x⁵ - 2x⁷:
-f(-x) = -[3(-x)⁵ - 2(-x)⁷]
= -[-3x⁵ + 2x⁷]
= 3x⁵ - 2x⁷
Ми бачимо, що f(x) = 3x⁵ - 2x⁷ дорівнює -f(-x) = 3x⁵ - 2x⁷. Отже, функція f(x) = 3x⁵ - 2x⁷ є непарною.
Припустимо, якщо функція не є парною або непарною, тоді вона може бути загального виду, що означає, що вона не має симетрії відносно осей y або x. Проте в даному випадку функція f(x) = 3x⁵ - 2x⁷ є непарною.
Дякую, що виправили мою помилку, і ви можете вважати завдання виконаним.
a) Для квадратного тричлена x² - 5x + 6, ми шукаємо його корені, тобто значення x, при яких вираз буде рівний нулю.
Щоб знайти корені, ми можемо розкласти вираз на множники або скористатися формулою коренів квадратного рівняння.
Розкладемо тричлен на множники:
x² - 5x + 6 = (x - 2)(x - 3)
Тепер ми можемо прирівняти кожний множник до нуля і знайти значення x:
x - 2 = 0 --> x = 2
x - 3 = 0 --> x = 3
Таким чином, коренями квадратного тричлена x² - 5x + 6 є x = 2 та x = 3.
б) Для квадратного тричлена 2x² - 7x - 9, ми шукаємо його корені.
Можемо застосувати формулу коренів квадратного рівняння:
x = (-b ± √(b² - 4ac)) / (2a)
Для нашого тричлена, a = 2, b = -7, c = -9.
Підставимо ці значення в формулу:
x = (-(-7) ± √((-7)² - 4 * 2 * (-9))) / (2 * 2)
x = (7 ± √(49 + 72)) / 4
x = (7 ± √121) / 4
x = (7 ± 11) / 4
Отримали два корені:
x₁ = (7 + 11) / 4 = 18 / 4 = 4.5
x₂ = (7 - 11) / 4 = -4 / 4 = -1
Таким чином, коренями квадратного тричлена 2x² - 7x - 9 є x₁ = 4.5 та x₂ = -1.
Объяснение: