Координаты точки пересечения графиков данных функций (-1; -1)
Решение системы уравнений х= -1
у= -1
Объяснение:
Решить графически систему уравнений
2x-y= -1
x+y= -2
Построить графики. Графики линейной функции, прямые линии. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
Прежде преобразуем уравнения в более удобный для вычислений вид:
2x-y= -1 x+y= -2
-у= -1-2х у= -2-х
у=1+2х
Таблицы:
х -1 0 1 х -1 0 1
у -1 1 3 у -1 -2 -3
Согласно графика, координаты точки пересечения графиков данных функций (-1; -1)
Решение системы уравнений х= -1
у= -1
Найдите множество значение функции f(x) = x^2+2x+19
ответ: D) (18, +∞)
Объяснение:
По формуле: -b:a= -3:1*3 = -2:3= -1 находим координаты Х вершины параболы х=-1
Подставляем в уравнении и находим координату У
(-1)² + 2*(-1) +19 = 1- 2 +19= -1+19 = 18
Вершина параболы находится в точки (-1;18)
Значит множество значений функции (18; +∞)
Найдите радиус окружности, длина которого 12 π см
Е) 6 см.
Объяснение:
Возьмем формулу длины окружности
l=2πr из этой формулы выведем радиус окружности
r=l/2π теперь подставим имеющиеся данные r=l/2π=12π/2π=6 cм

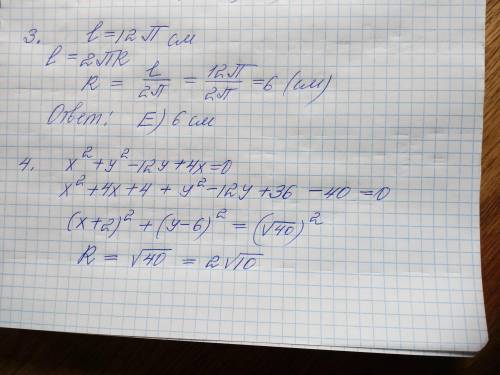
6x+15-6x-2=2
12x=-11
x=-11/12