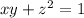относительно 
:
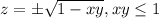
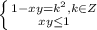
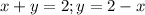
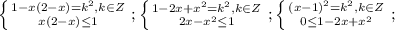
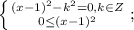
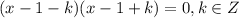
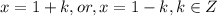
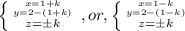
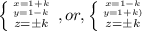
![\frac{a+b+c}{3} \geq \sqrt[3]{abc};a\ \textgreater \ 0;b\ \textgreater \ 0;c\ \textgreater \ 0](/tpl/images/0624/8535/ff736.png)
; 
; 
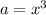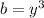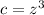
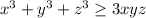
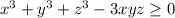
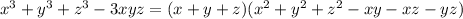
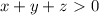по условию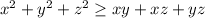
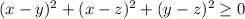
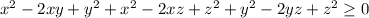
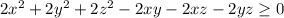
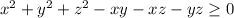
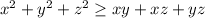
![\frac{a+b+c}{3} \geq \sqrt[3]{abc};a\ \textgreater \ 0;b\ \textgreater \ 0;c\ \textgreater \ 0](/tpl/images/0624/8535/603ee.png)
![a+b+c \geq 3\sqrt[3]{abc}=3* \sqrt[3]{1}=3](/tpl/images/0624/8535/40668.png)
Объяснение:
Смотри. Вторая часть выражения - это результат вычисления в первой части выражения. Значит, чтобы понять, какие числа пропущены во второй части, мы должны закончить действия в первой. Действия будут следующие:
0,1k^2u^4 : 0,5ku^3 = 0,2ku - это первое пропущенное число после 8k^2 (вторая звёздочка).
12,5ku^5 : 0,5ku^3 = 25u^2 - это второе пропущенное число после 8k^2 (третья звёздочка)
А чтобы узнать первую пропущенную звёздочку, мы просто должны совершить обратное действие с числом 8k^2. А именно:
8k^2 * 0,5ku^3 = 4k^3u^3 - это и есть первая пропущенная звёздочка.
Надеюсь, понятно объяснил ;)
P(A)=m/n
Событие А - "Приедет такси жёлтого цвета"
m=1 ( одна машина жёлтого цвета)
n=10 (всего машин 10)
Р(А)=1/10=0,1 (или 10%)