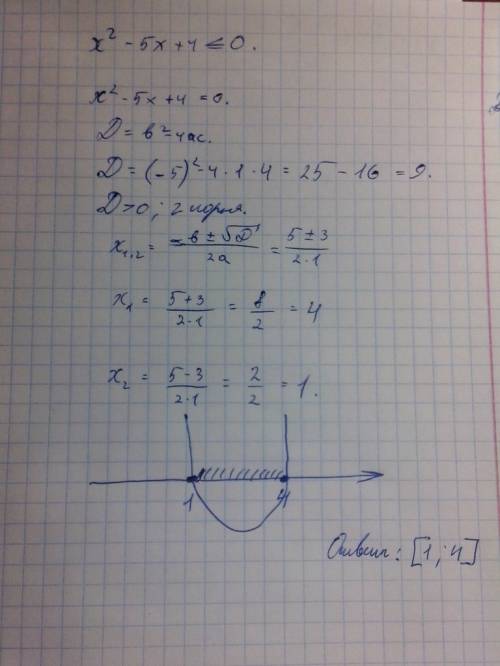
Определим общее число расстановок на пяти позициях 5 шариков:
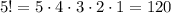
Однако, среди этих расстановок есть недопустимые (то есть те, при которых между зеленым и желтым шариком располагаются два или более шарика). Найдем число недопустимых расстановок.
Найдем число недопустимых размещений зеленого и желтого шарика. Их можно просто перечислить:
1) зеленый на 1-ом месте, желтый на 4-ом месте
2) зеленый на 1-ом месте, желтый на 5-ом месте
3) зеленый на 2-ом месте, желтый на 5-ом месте
4) зеленый на 4-ом месте, желтый на 1-ом месте
5) зеленый на 5-ом месте, желтый на 1-ом месте
6) зеленый на 5-ом месте, желтый на 1-ом месте
В каждом из этих случаев оставшиеся три шарика могут размещаться на свободных местах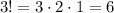 
Таким образом, всего имеется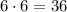 
недопустимых расстановок.
Значит, допустимых расстановок имеется:
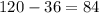
ответ: 84
Объяснение:
1. В примере а) коэффициенты k= равны 0,5, значит их графики параллельны.
В примере в) коэффициенты k=5, значит их графики параллельны.
2. ответ 3. Кубическая парабола, ветви графика расположены в 1 и 3 четвертях.
3. АБВГ
2413
4. 2x + y = 8
2x - y = 1
Из первого уравнения y = 8 - 2x. Тогда подставляем выражение во второе уравнение:
2x - (8 - 2x) = 1
2x - 8 + 2x = 1
4x = 9
x = 2,25
y = 8 - 2*2,25 = 8 - 4,5 = 3,5
ответ: (2,25; 3,5)
5. а) 1) y = 3x+1. Область определения функции - все действительные значения аргумента.
2) 
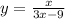. Область определения: 3x - 9 не равно нулю. Значит, x не равен 3. Следовательно, все, кроме 3.
б) 
при 
Если x = -5, то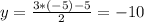 
Если х= 3, то 
Значит, 
