1) Рассмотрим команду (пусть это будет команда М), которая выиграла наименьшее количество встреч. Пусть это число равно 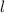 . Рассмотрим два случая:
. Рассмотрим два случая:
1. 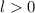 . Заметим, что количество побед этой команды равно количеству побежденных, а это число, в свою очередь, равно суммарному количеству побед побежденных. Очевидно, что каждый побежденный выиграл ровно 1 раз (если нет, то найдется хотя бы один побежденный с 0 побед, что противоречит минимальности). Значит,
. Заметим, что количество побед этой команды равно количеству побежденных, а это число, в свою очередь, равно суммарному количеству побед побежденных. Очевидно, что каждый побежденный выиграл ровно 1 раз (если нет, то найдется хотя бы один побежденный с 0 побед, что противоречит минимальности). Значит, 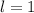 . Побежденный командой М тоже имеет 1 победу и так далее. Получим, что каждый победил ровно 1 раз. Поскольку каждый матч заканчивается чьей-то победой, то всего побед столько же, сколько и матчей. Суммарное количество побед равно
. Побежденный командой М тоже имеет 1 победу и так далее. Получим, что каждый победил ровно 1 раз. Поскольку каждый матч заканчивается чьей-то победой, то всего побед столько же, сколько и матчей. Суммарное количество побед равно 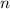 — числу участников (поскольку все победили 1 раз). Имеем:
— числу участников (поскольку все победили 1 раз). Имеем: 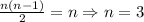 .
.
2. 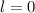 . Уберем команду М. Тогда количество побед каждой команды уменьшится на 1 (так как все победили команду М). Рассмотрим новую команду, имеющую наименьшее количество побед (
. Уберем команду М. Тогда количество побед каждой команды уменьшится на 1 (так как все победили команду М). Рассмотрим новую команду, имеющую наименьшее количество побед (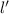 ). Если
). Если 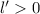 , то получим 3 команды + изъятая, то есть всего 4 команды. Если
, то получим 3 команды + изъятая, то есть всего 4 команды. Если  , то была команда с ровно одной победой. Продолжая рассуждения, получим, что была команда с хотя бы двумя победами, тремя и т.д. до
, то была команда с ровно одной победой. Продолжая рассуждения, получим, что была команда с хотя бы двумя победами, тремя и т.д. до  , то есть была команда, которая победила всех. Тогда
, то есть была команда, которая победила всех. Тогда 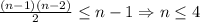 . Значит, могло быть либо три, либо четыре команды.
. Значит, могло быть либо три, либо четыре команды.
2) Пусть первая труба наполняет бассейн за 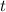 часов. Составим уравнение:
часов. Составим уравнение: 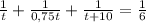 , откуда
, откуда 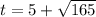 , остальные ищутся легко.
, остальные ищутся легко.
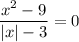
Дробь равна нолю, если ее числитель равен нолю, а знаменатель не равен:
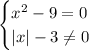
В первом уравнении 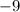 переносим вправо с изменением знака (или вспоминаем формулу разности квадратов:
переносим вправо с изменением знака (или вспоминаем формулу разности квадратов: 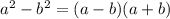 ), а во втором просто переносим
), а во втором просто переносим 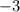 вправо:
вправо:
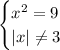
В первом уравнении  . А решением неравенства
. А решением неравенства 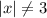 является
является 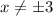 . Иначе говоря:
. Иначе говоря:
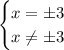

Таким образом, все корни, обнуляющие числитель обнуляют и знаменатель (а "делить на ноль нельзя"). Система уравнений получается слишком противоречивой (причем - не кому-то, а самой себе).
Значит, действительных решений у данного уравнения нет.
Это, конечно, можно было и не расписывать так подробно, а просто заметить, что ноль в числителе дают 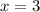 и
и  . Но они же и дают ноль в знаменателе!
. Но они же и дают ноль в знаменателе!
ответ: 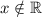 или
или 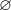
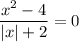
Здесь опять: числитель равен нолю, а знаменатель не равен.
Заметим, что 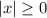 и
и 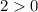 . Значит,
. Значит, 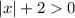 и знаменатель ни при каком значении
и знаменатель ни при каком значении  не равен нолю!
не равен нолю!
⇒ Достаточно, чтобы только числитель был равен нолю.
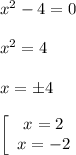
В общем, это и есть решение уравнения.
ответ: 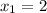 ,
,  .
.
_______________________________________________
Задание в)На всякий случай в) и е). В целом, они решаются абсолютно также, по аналогии, так что мои "объяснения" только испортят красоту решения уравнений.
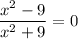

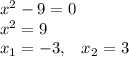
ответ:  ,
, 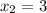
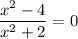

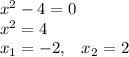
ответ:  ,
, 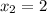
[√3*(√5-√3)(3*(√5+√3)+√3*(√5+√3))]/(√3-1)=[√3*(√5-√3)(√5+√3)(3+√3)]/(3-1)=[√3*((√5)²-(√3)²)(3+√3)]/(√3-1)=[√3*2*(3+√3)]/(√3-1)=[2√3(3+√3)(√3+1)]/[(√3-1)(√3+1)]=[2√3(3√3+√3*√3+3+√3)]/[3-1]=[2√2(4√3+6)]/2=12+6√3
квадратными скобками "отделяю" числитель и знаменатель