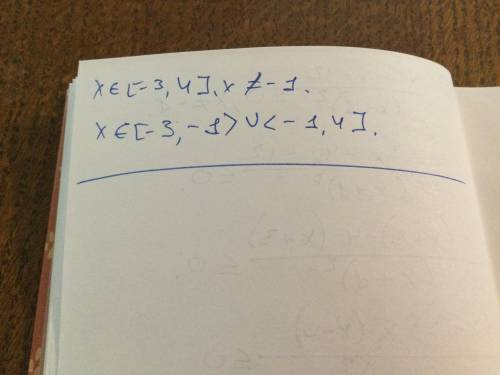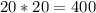
Объяснение:
А
х + 7у = -6 | * -2
2х - 5у = 7
-2х - 14у = 12
2х - 5у = 7
-19у = 19
2х - 5у = 7
1)
-19у = 19
у = 19 : (-19)
у = -1
2)
2х - 5у = 7
2х - 5*(-1) = 7
2х + 5 = 7
2х = 7 - 5
2х = 2
х = 2 : 2
х = 1
ответ: (1; -1)
Б
2х - 5у = 9
х + 4у = -2 | * -2
2х - 5у = 9
-2х - 8у = 4
-13у = 13
2х - 5у = 9
1)
-13у = 13
у = 13 : (-13)
у = -1
2)
2х - 5у = 9
2х - 5*(-1) = 9
2х + 5 = 9
2х = 9 - 5
2х = 4
х = 4 : 2
х = 2
ответ: (2; -1)
В
х - 2у = -7 | * -4
4х + 5у = 11
-4х + 8у = 28
4х + 5у = 11
13у = 39
4х + 5у = 11
1)
13у = 39
у = 39 : 13
у = 3
2)
4х + 5у = 11
4х + 5*3 = 11
4х + 15 = 11
4х = 11 - 15
4х = -4
х = -4 : 4
х = -1
ответ: (-1; 3)
Г
3х - 2у = 2
1/2х - 3у = -1/2 | * -6
3х - 2у = 2
-3х + 18у = 3
16у = 5
3х - 2у = 2
1)
16у = 5
у = 5 : 16
у = 5/16
2)
3х - 2у = 2
3х - 2*5/16 = 2
3х - 10/16 = 2
3х = 2 + 10/16
3х = 2. 10/16
3х = 42/16
х = 42/16 : 3
х = 42/16 * 1/3
х = 14/16 * 1/1
х = 14/16
х = 7/8
ответ: (7/8; 5/16)
1) (0; 5) ;
2) ( 4;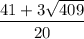 
)
3) [ - 3; - 1) ∪ ( -1; 4]
Объяснение:
Решить неравенства
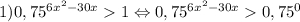
Так как основание степени 0<0,75 <1 , то показательная функция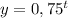 
убывающая.
Тогда получим
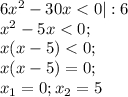
Определим знак ( во вложении) и получим
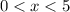, то есть х ∈ (0; 5).
ответ :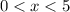
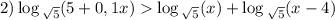
Так как логарифм определен на множестве положительных чисел, то найдем ОДЗ неравенства
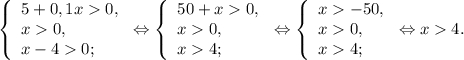
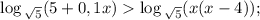
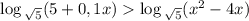
Так как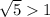 
, то логарифмическая функция 
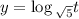возрастающая .
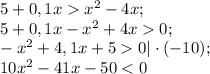
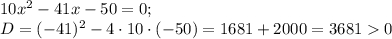
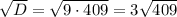
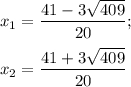
Определим знак ( во вложении)
Тогда
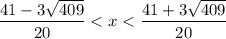
Учтем ОДЗ и получим
Так как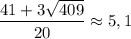 
, то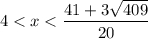 
ответ: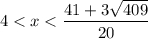
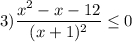
Разложим числитель на множители. Для этого решим квадратное уравнение
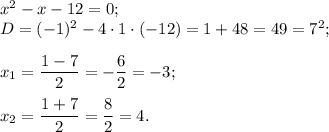
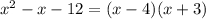
Тогда неравенство принимает вид:
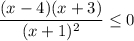
Решим неравенство методом интервалов .
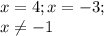
Определим знак ( во вложении)
Тогда получим
х ∈ [ - 3; - 1) ∪ ( -1; 4]
