Объяснение:
2.
a) 3x+12>4x-1 | (-x>-13) /-1 | x<13
7-2x<=10-3x | -3 <= -x /-1 | x <= 13. x принадлежит (-∞; 13].
б) 2x-9 > 6x+1 | (-4x > 10) / -4 | x<10
( -
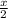< 2 ) *-2 | x > 4. x принадлежит (-∞; 10) и (4; +∞).
3.
а)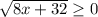 
Взводим все в квадрат
8x+32 => 0
8x => 32 делим все на 8
x => 4. x принадлежит [4; +∞).
б)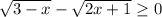 
Взводим все в квадрат
3-x-2x+1 => 0
4 => 3x Делим все на 3
1.3 => x
x <= 1.3. x принадлежит [-∞; 1.3).
4.
а-7 => 0 3-2a => 0
a => 7 3 => 2a
1.5 => a ответ: a принадлежит [7; +∞).
1) 99997 > 99988
ответ: 99997.
2) а) 8 + (72 - 42) = 8 + 30 = 38
б) 11 - (319 + 6) = 11 - 325 = - 314
3)
12 + 3 = 15 (км/ч) - скорость катера по течению реки.
15 * 3 = 45 (км) - катер проплыл по течению
12 - 3 = 9 (км/ч) - скорость катера против течения реки.
9 * 5 = 45 (км) - катер проплыл против течения.
45 + 45 = 90 (км) - катер проплыл за все время.
ответ: 90 км.
4)
3,8 (х + 1,3) = 9,5
3,8х + 3,8 * 1,3 = 9,5
3,8х + 4,94 = 9,5
3,8х = 9,5 - 4,94
3,8х = 4,56
х = 4,56 : 3,8
х = 1,2
Проверка:
3,8 (1,2 + 1,3) = 9,5
3,8 * 2,5 = 9,5
9,5 = 9,5
ответ: 1,2.
5) 1 ар = 100 м²
12 ар = 1200 м²
1200 : 30 = 40 (м) - длина участка.
ответ: 40 м.
f '(x) =(2x³ -x² +7x)' =6x² -2x +7;
f '(x₀) =6x₀² -2x₀ +7 =6(-1)² -2*(-1) +7 =15;
k=15.
2) f(x) =x² -8x+16 =(x-4)² ;x₁=a =1 ;x₂ =b=4 (границы интегрирования).
S =интеграл(1_4) (x-4)²dx =интеграл(1_4 (x-4)²d(x-4) =(x-4)³/3 |1_4
= (4-4)³/3 -(0-4)³/3 =64/3. границы интегрирования 1_4 =1-->4
S =интеграл(a_b)(x-4)²dx =интеграл(a_b)(x-4)²d(x-4) =(x-4)³/3 |a b =|| Формула Ньютона- Лейбница|| (b - 4)³/3 -(a - 4)³/3 = (4-4)³/3 -(0-4)³/3 =64/3.