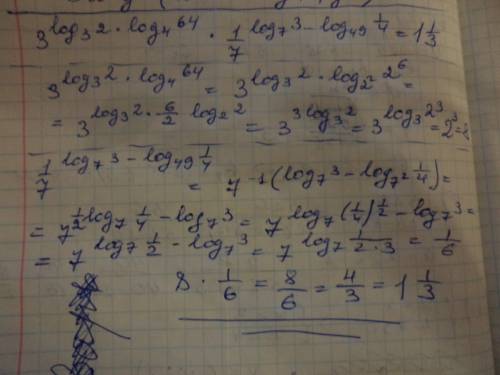
1.
а)x^3-2x = х(х²-2)
б)5a^2-10ab+5b^2 = 5(a^2-2ab+b^2) = 5(a-b)²
в)cm-cn+3m-3n = (cm-cn)+(3m-3n) = с(m-n)+3(m-n) = (с+3)(m-n)
2.
2(p+q)²-p(4q-p)+q² = 3p²+3q² при любых p и q
2(p+q)²-p(4q-p)+q² = 2(p²+2pq+q²) -4pq+p²+q² = 2p²+4pq+2q² -4pq+p²+q² = 3p²+3q²
таким образом, мы привели левую часть к правой, тем самым доказав, что значения выражений будут равны при любых p и q
3.
(x-3)(x+3) = x(x-2)
х²-9=х²-2х
2х=9
х=4,5
ответ: при х=4,5
4.
а)(a-3b)(a+3b)+(2b+a)(a-2b) = (a²-9b²) + (a²-4b²) = 2a²-13b²
б)(p+q)(q-p)(q²+p²) = (q²-p²)(q²+p²) = q⁴-p⁴
5.
x³-27-3x(x-3)=0
(x³-3³)-3x(x-3)=0
воспользуемся формулой разности кубов:
(х-3)(х²+3х+9)-3x(x-3)=0
(х-3)(х²+3х+9-3х)=0
х-3=0 или (х²+3х+9-3х)=0
х=3 х²+9=0
х²=-9 - решений нет
ответ: х=3
71.
1) 0.7√100-1/3√36= 0.7*10-1/3*6=7-6/3=7-2=5
2)√16*√0.25+√5³-4=4*0.5+√125-4=2+√121=2+11=13
3)3√0.81-√9²+12²=3*0.9-√81+144=2.7-√225=2.7-15=-12.3
4)√7 1/9+√3 1/16 - 0.04√90000= √64/9+√49/16-0.04*300=8/3+7/4-12=2 2/3+1 3/4-12
72.
1)(√11)²-√1.44=11-1.2=9.8
2)(2√13)²-(5√8)²=2*13-5*8=26-40=-14
3)14(-1/7√15)²-1/8(2√6)²=14(-1/7*15)-1/8(2*6)=14*(-15/7)-1/8*12=-210/7-12/8=-30-1.5=-31.5
4)√529-(1/2√84)²=23-(1/2*84)=23-84/2=23-42=-19
Объяснение:
71.
1)1*6/3(дробь)=6/3(сокращаем дробь)=2/1(1 не пишем)
/ - обозначение дроби.
Жирные числа - обозначение целых (7(7 целых),3(целых))