Объяснение:
выражение в квадратном корне должно давать положительный результат, иначе выражение не
имеет смысла
1) √х. х не должен быть –1 или каким-то другим отрицательным числом, поэтому выражение имеет смысл при х (0; +∞)
2) √х². Здесь х также может быть и отрицательным, поскольку он возведён во вторую степень, которая даёт положительный результат в любом случае поэтому: х (–∞; +∞)
3) √–х. х не должен быть положительным, поскольку при положительном х у нас получится отрицательный итог, например при х=1 =√–1, это недопустимо, поэтому х должен быть: х≤0 и значение следующие: х (–∞; 0)
5) √25х. х должен быть 0 или положительное значение:
х≥0, поэтому х (0; +∞)
4) √–3х. х должен быть отрицательным, чтобы выражение давало положительный результат:
х (–∞; –1)
6) √0,01х, х≥0; х (0; +∞)
7)
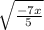
х ≥ 0; х (–∞; 0)
8)
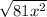
х может быть как положительным так и отрицательным, поскольку он возведён во вторую степень и значение выражения всегда будет положительным: х (–∞; +∞)
а у(км/ч)-собственная скорость катера.
Тогда скорость катера по течению реки равна (х+у)км/ч, а против течения (у-х)км/ч.По условию по течению катер км), т.е. 5/3х+5/3у(км), а против течения 24(км),т.е. 1,5у-1,5х(км).
Составим и решим систему уравнений: (5/3 - это 1ч 20мин)
5/3х+5/3у=28, умножаем на 3
1,5у-1,5х=24; умножаем на 10
5х+5у=84,
15у-15х=240;делим на 3
5х+5у=84,
5у-5х=80;
решаем сложения
10у=164,
5у-5х=80;
у=16,4;
5*16,4-5х=80,
у=16,4;
-5х=80-82,
у=16,4;
-5х=-2,
у=16,4;
х=0,4,
у=16,4.
0,4(км/ч)-скорость течения реки