Объяснение:
1) ОДЗ: 2x+1>0, x>-1/2 u 3x-7>0, x>7/3, основания равны, 2x+1=3x-7, x=8
2) ОДЗ: x>0 u x+2>0, x>-2, значит, x>0,
log2 (x*(x+2))=3, x^2+2x=2^3, x^2+2x-8=0, корни х=2 и х=-4(не
удовлетворяет ОДЗ), отв. х=2
3)обозначим lgx=t/ x>0, t^2-3t+2=0, t=1 u t=2, тогда, lgx=1, x=10,
lgx=2, x=10^2=100, отв: 10 и 100 (^ -знак степени)
1) ОДЗ: 4x+3>0, x>-3/4, т.к. основание >1, то 4x+3>16^ 1/2,
4x+3>4, 4x> 1, x> 1/4
2) ОДЗ: х>0, пусть t=log4 x, тогда, t^2-2t-3<0, , корни t=3 u t=-1,
-1<t<3, -1<log4 x<3, 1/4<x<4^3, 1/4<x<64
Объяснение:
0,0036=3,6 * 10¯³
если мы в записи числа 3,6 передвинем запятую влево на 3 цифры(т.е умножаем на 0,001),то вместо числа 3,6 получим 0,0036
давай еще пару примеров
0,045 =4,5 *10¯² передвинули запятую на 2 цифры(т.е умножаем на 0,01)поэтому 10 в минус 2 степени
0,000079=7,9*10¯⁵ передвинули запятую на 5 цифр(т.е умножаем на 0,00001),поэтому 10 в минус 5 степени
теперь немного другие примеры
7900000=7,9*10⁶ здесь запятую будем переносить вправо на 6 цифр(т.е умножаем на 1 000 000) поэтому 10 в 6 степени
2700=2,7*10³; 95000=9,5*10⁴; 420000000=4,2*10⁸
2.
А¹⁰*А⁻⁷=А¹⁰⁺⁽⁻⁷⁾=А³ здесь действительно должно быть плюс 3(при умножении степеней с одинаковым основанием показатели складываются)
3 задание смотри внизу.
а вот Условие 4) и 5 ) заданий не понятно записаны.
в 4)если надо решить уравнение √х = 3 то тогда получим ответ х=9,а если х²=3 то тогда х1 =- √3, х2=√3
и 5) 2/2√3 = 2√3/2 √3:√3= 2 √3/2 √3² ( тут сокращение) =√3/3 и тут не понятно,какое именно задание,похоже,что надо избавиться от корня в знаменателе.Если это так,напиши,я редактирую ответ и объясню и эти задания
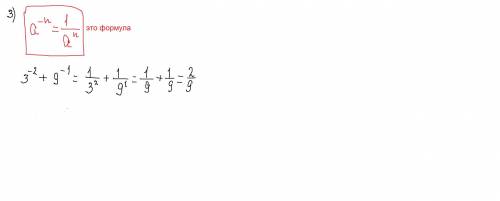
выбрать дежурного - это событие, а число возможных исходов (возможностей) равняется числу учеников в классе, 7=14-21.
по условию задачи происходит множество событий (два). их вероятность состоит из вычисления вероятностей нескольких отдельных событий.
эти два события связанные, т.к. первое событие влияет на второе. выбор девочки исключает ее из числа возможностей и уменьшает количество участвующих в выборе учеников класса.
с теорией закончили. перейдем к практическому решению задачи.
вероятность выбора девочки в качестве дежурной равняется 14/21=2/3
повторный выбор девочки в качестве дежурной будет уже равняться 13/20
общая вероятность выбора дежурными двух девочек равна произведению вероятностей связанных событий 2/3*13/20=26/60=0,04(3)≈0,433=43,3%