2503,2 I_56 0,414 I_43
- 224 44,7 - 387 0, 009623
263 270
- 224 - 258
392 120
- 392 - 86
0 140
- 129
11 (остаток) дальше смысла нет делить.
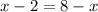
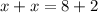
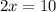
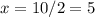
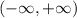 , но не принадлежит
, но не принадлежит 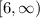 ,
, ![(-\infty, 0]](/tpl/images/0408/1975/03e35.png) ,
, 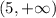 .
.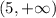 . Тут круглая скобка перед 5 означает, что точка x=5 исключена "вырезана" из интервала, а квадратная означает, что точка включена в интервал. Вот, например x=5 принадлежит интервалу
. Тут круглая скобка перед 5 означает, что точка x=5 исключена "вырезана" из интервала, а квадратная означает, что точка включена в интервал. Вот, например x=5 принадлежит интервалу 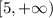 . Если обе крайние точки принадлежат интервалу, то насколько мне помнится его называют "отрезок".
. Если обе крайние точки принадлежат интервалу, то насколько мне помнится его называют "отрезок".
y ' = (x^4 - 4x^3+10) ' =(x^4) ' - (4x^3)'+(10) ' =4x³ -4(x³)' +0 =4x³ -4*3*x² = 4x²(x-3) ;
Определим участки монотонности .
участки убывания : y ' < 0 ;
4x²(x-3) < 0 ⇒x< 3 иначе x∈(-∞ 3) .
участки возрастания : y ' > 0 ;
4x²(x-3)> 0 ⇒x>3 иначе x∈(3 ∞) .
критические точки x =0 и x=3 .
точки экстремума :
При переходе через x=0 y ' не меняет знак.
x=3 точка минимума ( знак y ' " - " ==>" + " ) .
x= 0 точка перегиба.