Перенесем все на координатную плоскость. Пусть точка Н = (0,0), точка А лежит на оси Оу. На скрине А(0,7), В(0,4), а рассматривать мы будем любые А(0, а) и В(0,b).
Получается, одна прямая проходит точку А и точку (-k, 0) а другая - B и (k,0), при чем мы рассматриваем всевозможные k. Здесь k - расстояние от точки Н до точки С и D.
Кстати говоря, условие, что точка В должна быть между А и Н необязательно, можно взять и точку А между В и Н, на решение это не влияет в силу симметриии, главное, что бы обе точки лежали на перпендикуляре (то есть на оси Оу).
Запишем уравнение прямых.
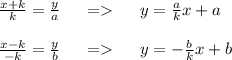
Так как нас интересует пересечение - приравниваем:
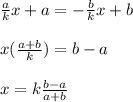
Поскольку пересечение двух прямых точно лежит на каждой из них, нужно подставить полученный икс в уравнение любой из прямых, результат будет одинаков.
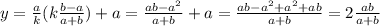
Получилось, что для любого k, то есть для любого расстояния между точкой H до С и D, мы находим зависимый от k икс, и независимый от k игрек. То есть как бы мы не раздвигали точки C и D, игрек будет всегда один и тот же, зависящий только от точек А и В, на которые мы "привязываем" прямые AD и BC.
Итого, ответ - прямая 
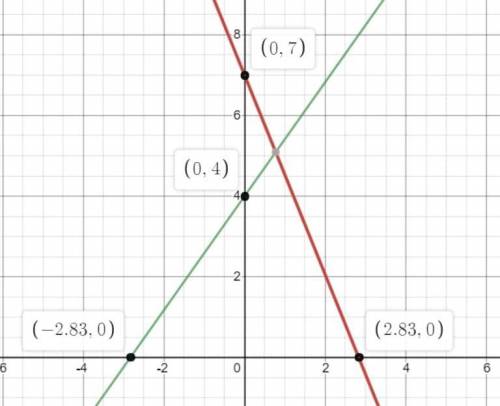
4
Объяснение:
Первым делом пользуемся методом исключения:
в условии сказано, что разность между цифрами должна быть равна 2, просматриваем все варианты и понимаем, что ответы под номерами 1 и 2 не подходят (в первом варианте 9 и 7 подходят по данному условия, а -9 и 7 нет, так как разность равна 16; во втором варианте тоже самое: разность первых двух цифр равна 2, а разность двух последующих цифр равна 14, значит не подходит)
У нас остались два варианта, это 3 и 4. Чтобы найти ответ смотрим ещё одно условие: Сумма квадратов двух чисел больше произведение на 39. Теперь просто каждый оставшийся вариант пробуем преобразовать в это условие.
3) 8 и 6 или -8 и -6
8^2 + 6^2 = 64 + 36 = 100
8 × 6 = 48
100 - 48 = 52 (а должно быть 39, значит уже не подходит и вторую пару цифр считать не надо)
4) 7 и 5 или -7 и -5
7^2 + 5^2 = 49 + 25 = 74
7 × 5 = 35
74 - 35 = 39 (подходит)
(-7)^2 + (-5)^2 = 49 + 25 = 74
(-7) × (-5) = 35
74 -35 = 39 (подходит)
Обе пары цифр в данном варианте подходят по всем условиям задачи, значит, ответ под номером 4 верный