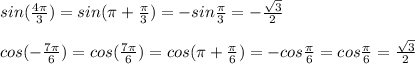
Для решения задачи необходимо определить производительность работы каждой из труб.
Представим весь объем воды в бассейне в виде 100% или 1.
В таком случае, за 1 час работы первая труба наполнит:
1 / 10 = 1/10 часть бассейна.
Вторая труба наполнит:
1 / 8 = 1/8 часть бассейна.
Находим продуктивность работы двух труб при совместной работе.
Для этого суммируем продуктивность каждой трубы.
1/10 + 1/8 = (Общий знаменатель 40) = 4/40 + 5/40 = 9/40.
В таком случае, после 1 часа совместной работы останется наполнить:
1 - 9/40 = 31/40 часть бассейна.
Для начала выразим в данном уравнении одну переменную через другую. Например, переменную  через переменную
через переменную 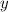 .
.
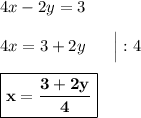
Для каждой пары решений этого уравнения данное равенство будет выполняться. Теперь берём для переменной 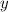 любое значение, которое захотим, подставляем в выражение сверху и находим переменную
любое значение, которое захотим, подставляем в выражение сверху и находим переменную  . Возьмём, например,
. Возьмём, например, 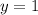 , получится:
, получится:
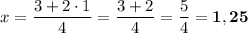 .
.
Таким образом, пара чисел 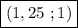 является решением нашего уравнения. Подставим, например,
является решением нашего уравнения. Подставим, например, 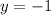 :
:
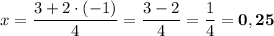 .
.
И ещё одну пару чисел, 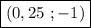 , мы получили. И для последней пары мы возьмём, к примеру,
, мы получили. И для последней пары мы возьмём, к примеру, 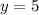 :
:
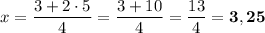 .
.
И получили последнюю пару чисел: 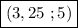 .
.