1)
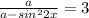
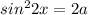
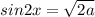
Так как значения синуса не могут быть большими единицы, получаем:
Так как выражение под радикалом и собственно весь радикал не могут быть отрицательными получаем:
Откуда получаем:
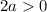
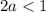
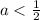
Объединяя полученные результаты получаем: a∈
ответ: a∈
2)
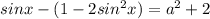
Получаем квадратное уравнение относительно t:
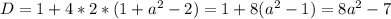
Исходя из того что данное уравнение должно иметь лишь одно решение получаем, что дискриминант должен быть равен нулю:
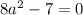
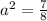
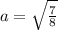
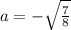
Но так как нам нужно только одно решение в заданном промежутке получаем:
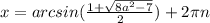
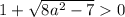
неравенство не имеет решений
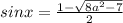
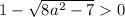
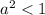
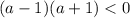
Получаем, что при a∈
данное уравнение имеет лишь один корень
ответ: a∈
Уравнение параболы y=ax^2+bx+c
Так как парабола проходит через точку А(8;-2), то
-2=64а+8b+c (1)
Координаты вершины параболы (2;4), через неё парабола тоже, логично, проходит, поэтому
4=4а+2b+c (2)
А также абсцисса вершины параболы определяется по формуле
x=-b/2a => 2=-b/2a, 4a=-b,
4a+b=0 (3)
Работаем с выражениями (1), (2) и (3):
(1-2) -6=60а+6b; 36a+6*(4a+b)=-6;
Т.к. 4a-b=0, то 36a=-6; a=-1/6
(3) 4a=-b; 2/3=b
Подставляем найденные значения а и b в выражение (2)
4=-4/6 + 4/6 + с, с=4
Поэтому искомое уравнение параболы
ответ: - 1/6 x^2 + 2/3 x + 4
Δ
ответ: