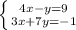
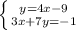
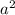 -9ab=3a(a-b)
-9ab=3a(a-b)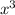 -25x=x(
-25x=x(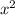 -25)=x(x-5)(x+5)
-25)=x(x-5)(x+5)
56 = 8 + 18 + 2с;
2с = 56 - 26;
2с = 20
с = 20/2;
с = 10
Площадь равнобедренной трапеции можно найти, зная все ее стороны, по формуле:
S = 1/4 √((a + b)^2(a - b + 2c)(b - a + 2c)).
Подставим известные значения и найдем площадь трапеции:
S = 1/4 √((8 + 18)^2(8 - 18 + 2*10)(18 - 8 + 2*10)) = 1/4 √(26^2(26 - 10)(26 + 10)) = 26/4 √(26^2 - 10^2) = 13/2 √(676 - 100) = 10/2 √576 = 10/2 * 24 = 10 * 12 = 156 (условных единиц квадратных).
ответ: S = 156 условных единиц квадратных.
Объяснение:
Вроде бы так
4х-у=9 -у=9-4х у=4х-9
3х+7у=-1 3х+7у=-1 3х+7(4х-9)=-1
3х+28х-63+1=0
31х=62
х=2
у=-1
2)
3а^2-9ab= 3a(a-3b)
x^3-25x=x(x^2-25)=x(x-5)(x+5)