Дана арифметическая прогрессия -15, -12, ..., то есть a₁= -15, a₂= -12. Тогда
а) её разность:
d = a₂ - a₁ = -12 - (-15) = -12 + 15 = 3.
б) формула n-члена этой прогрессии :
a(n) = -15+3·(n-1)
в) выясним, содержится ли в этой прогрессии число 12:
a(n) = 12 или
-15+3·(n-1) = 12
3·(n-1) = 12 + 15
3·(n-1) = 27
n-1 = 27:3
n = 9+1=10∈N
Содержится под номером 10.
г) Так как d=3 >0, то в этой прогрессии бесконечное количество положительных членов. В самом деле:
a(n) = -15+3·(n-1)>0
3·(n-1)>15
n-1>15:3
n>5+1
n>6
Начиная с 7-члена арифметической прогрессии все члены положительные. Так как множество натуральных чисел N бесконечно, то положительных членов арифметической прогрессии бесконечно.
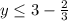
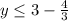
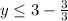
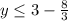
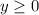
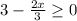

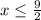
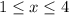
2х - 8 = 2( х - 4)
12х - 48 = 12( х - 4)
теперь будем делать в скобках . надо привести к общему знаменателю. Общий знаменатель = 6(х - 4) . к 1 дроби дополнительный множитель = 2, ко 2-й дополнительный множитель = 3. В скобке получим:
(3х - 2 - 3х + 9)/6( х - 4) = (7 - х)/6( х - 4)
Теперь этот результат надо умножить на 12(х - 4)/(7 - х)
Видно, что после сокращения останется 2
ответ:2