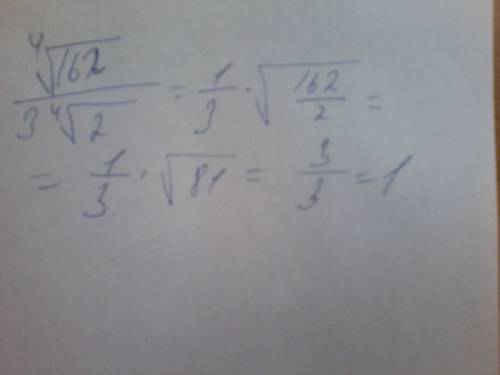
Минимальное n=51
Объяснение:
n^3+7^(2050)=n^3+ 49^(1025)=n^3+(50-1)^1025
(50-1)^(1025) -разложение бинома ньютона ,в котором все члены содержащие 50^2 кратны 100. Последний член равен: (-1)^1025=-1
А предпоследний равен 50*k . Тк степень 1025 нечетна,то согласно разложению бинома предпоследний коэффициент n нечетен. (все остальные члены содержат степень 50^2 cоответствено кратны 100)
Тогда 50*n ,кончается на 50,то есть остаток от деления на 100 этого числа равен 50.
А общий остаток от деления числа
(50-1)^1025 на 100 равен: 50-1=49
Соответственно:
n^3+49 должно быть кратно 100
Нужно отыскать минимальное n^3 которое кончается на 51
n^3=100*k +51 k-натуральное число
n^3=50*(2k+1)+1
Так же очевидно, что 51^3=(50+1)^3 кончается на 51 тк 3 нечетное число,это следует из тех же рассуждений что и в (50-1)^1025 ,только тут 1^3=1 ,следовательно кончается на 51 (дает остаток 51 при делении на 100). Очевидно, что n=51 самый вероятный кандидат на минимальное n.
Осталось доказать , что натуральное число n<51 (возведенное в куб не может оканчиваться на 51)
Предположим что такое число существует, тогда
очевидно что : n=(10*r+1) r<5 ,тк число должно кончатся на цифру 1.
Тк только цифра 1^3 кончается на 1.
(10*r+1)^3=50*(2k+1) +1
(10*r+1)^3 -1^3=50*(2k+1) (применим формулу разности кубов) n^3-1^3=(n-1)*(n^2+n+1)
(10*r)*( (10*r+1)^2 +10*r+2)=50*(2k+1)
r*(100*r^2 +30r +3)=5*(2k+1) ,то есть левое число должно делится на 5.
Очевидно ,что 100*r^2+30*r+3 не делится на 5 тк все члены кроме трех кратны пяти. Откуда .поскольку число 5 простое,то r должно быть кратно 5, но r<5 ,то есть r не может быть кратно 5.
Мы пришли к противоречию,то есть такое невозможно.
Вывод: n=51
.
.
.
. Но 
фактически лишнее неравенство, оно выполняется автоматически потому, что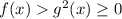 
, ибо полный квадрат всегда неотрицателен.
