Найдите cosa,если sina= - корень квадратный из 3/2 и а принадлежит ( п; 3п/2)

👇

Увидеть ответ

Ответ:

Lolla20031999

27.01.2023

cosa=sin(П/2-a)=-sinП/6=-1/2

4,8(47 оценок)

Открыть все ответы

Ответ:

sofiaivkina84

27.01.2023

Метод Феррари:

уравнение вида

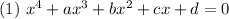
$(1)\ x^4+ax^3+bx^2+cx+d=0$

с замены 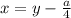$x=y-\frac{a}{4}$

приводим к виду

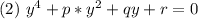
$(2)\ y^4+p*y^2+qy+r=0$

где:

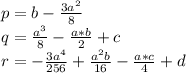
$p=b-\frac{3a^2}{8}\\q=\frac{a^3}{8}-\frac{a*b}{2}+c\\r=-\frac{3a^4}{256}+\frac{a^2b}{16}-\frac{a*c}{4}+d$

добавим и вычтем из левой части уравнения 2 выражение 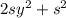2sy^2+s^2 , где s - некоторое число: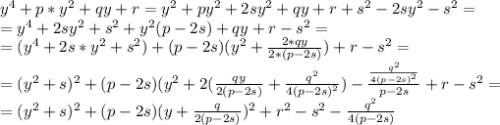 $y^4+p*y^2+qy+r=y^2+py^2+2sy^2+qy+r+s^2-2sy^2-s^2=\\=y^4+2sy^2+s^2+y^2(p-2s)+qy+r-s^2=\\=(y^4+2s*y^2+s^2)+(p-2s)(y^2+\frac{2*qy}{2*(p-2s)})+r-s^2=\\=(y^2+s)^2+(p-2s)(y^2+2(\frac{qy}{2(p-2s)}+\frac{q^2}{4(p-2s)^2})-\frac{\frac{q^2}{4(p-2s)^2}}{p-2s}+r-s^2=\\=(y^2+s)^2+(p-2s)(y+\frac{q}{2(p-2s)})^2+r^2-s^2-\frac{q^2}{4(p-2s)}$

получим:

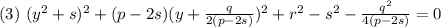
$(3)\ (y^2+s)^2+(p-2s)(y+\frac{q}{2(p-2s)})^2+r^2-s^2-\frac{q^2}{4(p-2s)}=0$

Пусть s - корень уравнения

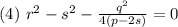
$(4)\ r^2-s^2-\frac{q^2}{4(p-2s)}=0$

Тогда уравнение 3 примет вид:

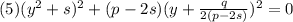
$(5)(y^2+s)^2+(p-2s)(y+\frac{q}{2(p-2s)})^2=0$

Избавляемся в уравнении 4 от знаменателя:

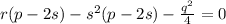
$r(p-2s)-s^2(p-2s)-\frac{q^2}{4}=0$

Раскроем скобки и получим:

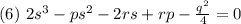
$(6)\ 2s^3-ps^2-2rs+rp-\frac{q^2}{4}=0$

Уравнение 6 называется кубической резольвентой уравнения 4 степени.

Разложим уравнение 5 на множители:

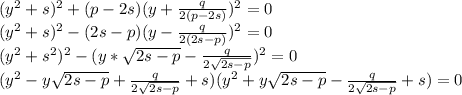
$(y^2+s)^2+(p-2s)(y+\frac{q}{2(p-2s)})^2=0\\(y^2+s)^2-(2s-p)(y-\frac{q}{2(2s-p)})^2=0\\(y^2+s^2)^2-(y*\sqrt{2s-p}-\frac{q}{2\sqrt{2s-p}})^2=0\\(y^2-y\sqrt{2s-p}+\frac{q}{2\sqrt{2s-p}}+s)(y^2+y\sqrt{2s-p}-\frac{q}{2\sqrt{2s-p}}+s)=0$

Получим два квадратных уравнения:

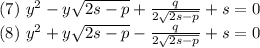
$(7)\ y^2-y\sqrt{2s-p}+\frac{q}{2\sqrt{2s-p}}+s=0\\(8)\ y^2+y\sqrt{2s-p}-\frac{q}{2\sqrt{2s-p}}+s=0$

Применяем этот метод для решения уравнения:

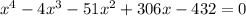
$x^{4} -4x^{3} -51x^{2} +306x-432=0$

коэффициенты:

a=-4

b=-51

c=306

d=-432

Определяем p,q и r:

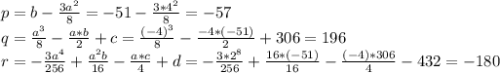
$p=b-\frac{3a^2}{8}=-51-\frac{3*4^2}{8}=-57 \\q=\frac{a^3}{8}-\frac{a*b}{2}+c=\frac{(-4)^3}{8}-\frac{-4*(-51)}{2}+306=196 \\r=-\frac{3a^4}{256}+\frac{a^2b}{16}-\frac{a*c}{4}+d=-\frac{3*2^8}{256} +\frac{16*(-51)}{16} -\frac{(-4)*306}{4} -432=-180$

Ищем s:

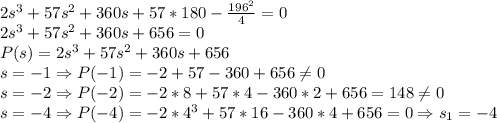
$2s^3+57s^2+360s+57*180-\frac{196^2}{4}=0\\2s^3+57s^2+360s+656=0\\P(s)=2s^3+57s^2+360s+656\\s=-1\Rightarrow P(-1)=-2+57-360+656\neq 0\\s=-2\Rightarrow P(-2)=-2*8+57*4-360*2+656=148\neq 0\\s=-4\Rightarrow P(-4)=-2*4^3+57*16-360*4+656=0 \Rightarrow s_1=-4$

Возможно, у этого уравнения третьей степени есть и другие действительные корни. Но для данной задачи находить их все не обязательно. Достаточно одного корня, т.е числа, при котором выражение обращается в ноль.

Подставляем p,q,r и s в квадратные уравнения 7 и 8:

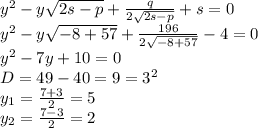
$y^2-y\sqrt{2s-p}+\frac{q}{2\sqrt{2s-p}}+s=0\\y^2-y\sqrt{-8+57}+\frac{196}{2\sqrt{-8+57}} -4=0\\y^2-7y+10=0\\D=49-40=9=3^2\\y_1=\frac{7+3}{2}=5\\y_2=\frac{7-3}{2}=2$

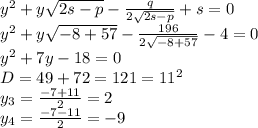
$y^2+y\sqrt{2s-p}-\frac{q}{2\sqrt{2s-p}}+s=0\\y^2+y\sqrt{-8+57}-\frac{196}{2\sqrt{-8+57}} -4=0\\y^2+7y-18=0\\D=49+72=121=11^2\\y_3=\frac{-7+11}{2}=2\\y_4=\frac{-7-11}{2}=-9$

Находим x:

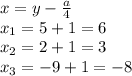
$x=y-\frac{a}{4} \\x_1=5+1=6\\x_2=2+1=3\\x_3=-9+1=-8$

ответ: -8; 3; 6

4,4(99 оценок)

Ответ:

ksenia112005

27.01.2023

1. Достраиваем исходный прямоугольный треугольник до прямоугольника.
2. Проводим вторую диагональ получившегося прямоугольника.
3. Получилось четыре одинаковых прямоугольных треугольника.
4. Разбиваем прямоугольник на четыре равных прямоугольника проводя параллельные прямые через точку пересечения диагоналей.
5. Получившиеся прямоугольники имеют наибольшую площадь так как в сумме дают полную площадь прямоугольника.
6. Площадь прямоугольника 8*5=40 см².
7. Площадь вписанного прямоугольника 40/4=10 см².

4,6(68 оценок)

Это интересно:

Компьютеры-и-электроника

28.03.2021

Как удалить историю веб поиска в Google: простые шаги для защиты вашей конфиденциальности...

Компьютеры-и-электроника

27.03.2021

Как поймать Суикуна в игре Покемон - Кристальная версия...

Образование-и-коммуникации

07.08.2020

Как нарисовать собачью морду: советы и инструкции...

Компьютеры-и-электроника