Объяснение:
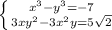
сложим эти два уравнения и преобразуем по формуле куба разности:

Для простоты вычислений введём константу С
![C=\sqrt[3]{5\sqrt{2}-7 }](/tpl/images/2018/3457/220b9.png)
C≈0,4142
Из последнего выражения имеем следующие тождества
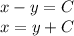
Подставляем x в первое уравнение
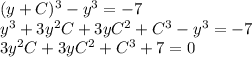
В последнее С³ подставим его значение, чтобы сократить семёрку.
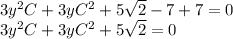
Теперь решаем обычное квадратное уравнение
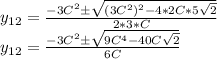
Тут получается что дискриминант отрицательный и корней нет.
Вариант второй, графический
из первого уравнения получаем график функции
![y=\sqrt[3]{x^{3} +7} \\](/tpl/images/2018/3457/4771c.png)
А из второго
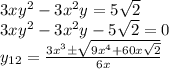
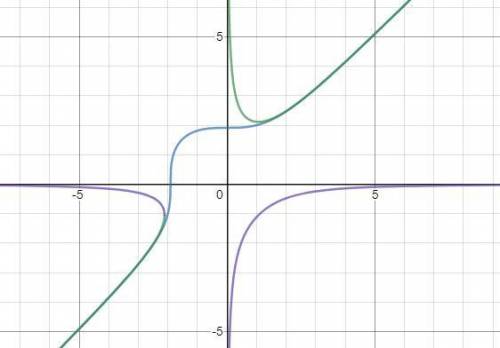
Строим графики.
Видим, что точек пересечения нет.
Графики стремятся приблизится друг к другу, но не пересекаются
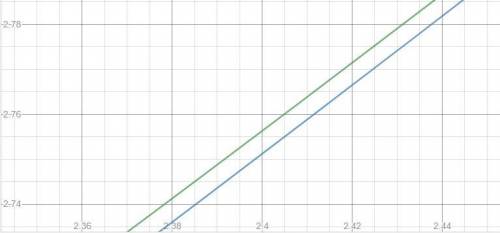
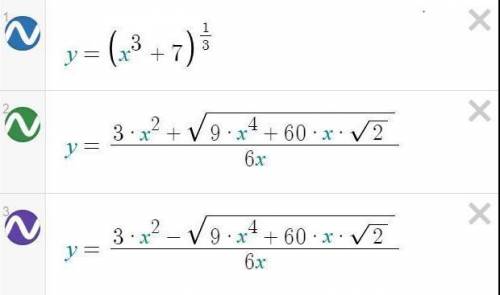
1)8х²-12х+36=0
D=(-(-12))²-4×8×36=144-1152=-1008
D<0, решения нет.
3х²+32+80=0
3x²+112=0|÷3
x²+37,33=0
x²=-37,33 Решения нет, так как любое число в квадрате не может быть отрицательным.
2)3x^2 + 32x + 80 = 0;
D = b^2 - 4ac, где:
ах^2 + bx + c = 0;
D = 32^2 - 4 * 3 * 80 = 1024 - 12 * 80 = 1024 - 960 = 64.
Сейчас найдем корень квадратный из дискриминанта:
√D = √64 = 8.
Найдем корни уравнения:
х1 = (-b + √D)/2a = (-32 + 8)/2 * 3 = -24/6 = -3 - первый корень уравнения.
х1 = (-b - √D)/2a = (-32 - 8)/2 * 3 = -40/6 = -6,67 - второй корень уравнения.
3)12y^2+16y-3=0
D1= 8^2-12*(-3)=64+36=100
y1=-8+10=2
y2=-8-10=-18
найдем нули функции
x=1
x= - 1 не входит в промежуток
x≠0
y(1/2)=2.5
y(1)=2
y(2)=2.5
y(1/2)=y(2)=2.5 - наибольшее значение
y(1)= 2 - наименьшее