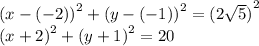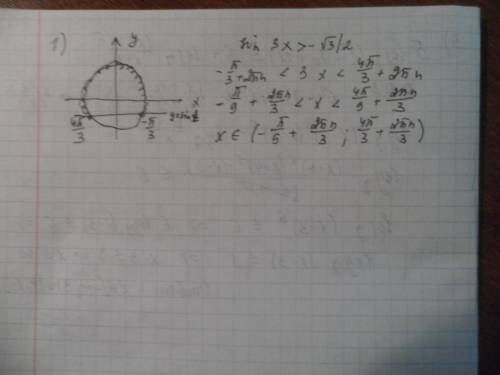
ответ: 19.
Объяснение: найдем первый член последовательности: 1² + 2 × 1 = 3.
Сумма двух первых членов равна 2² + 2×2 = 8. Тогда второй член равен 8 - 3 = 5.
Сумма трех первых членов: 3² + 2 × 3 = 15. Тогда третий член равен 15 - 5 - 3 = 7.
Заметим, что каждый новый член отличается от предыдущего ровно на 2 единицы: u1 = 3, u2 = 3 + 2 = 5, u3 = 5 + 2 = 7. Тогда последовательность Un - арифметическая прогрессия с разностью d = 2, что и требовалось доказать.
По формуле общего члена арифм. прогрессии найдем девятым член:
u9 = u1 + 8d = 3 + 8 × 2 = 19.
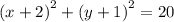
Объяснение:
заданная точка принадлежит прямой
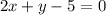
перпендикуляры к заданным прямым будут описываться формулой соответственно:
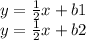
так как коэффициенты при x одинаковы, сами прямые и их перпендикуляры параллельны, поэтому перпендикуляр проходящий через точку (2,1) будет проходит через центр окружности и пересекать точку касания первой прямой. уравнение этого перпендикуляра найдем подставив x и y
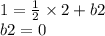
значит перпендикуляр пересекающий точки касания и центр окружности
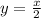
точка касания первой прямой:
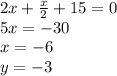
тогда центр окружности лежит посредине двух точек касания и получаем:
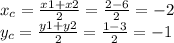
расстояние между этими точками равно двум радиусам, поэтому:

поэтому уравнение окружности: