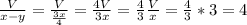
Все гири имеют различный вес, назовём их в порядке возрастания веса: g₁<g₂<g₃<g₄<g₅. Гири весят натуральное число грамм, поэтому минимальная разница между гирями 1г.
В решении я не буду использовать другие ед. измер., только граммы, поэтому, для упрощения записей, я не буду писать гр.
Пусть минимальный воможный вес для g₁ это x. Тогда: для g₂ - x+1; g₃ - x+2; g₄ - x+3; g₅ - x+4.
Самый минимальный суммарный вес для трёх гирь можно собрать из g₁ , g₂ , g₃ ; а самый максимальный для двух - g₄ , g₅.
Любые три гири весят больше, чем две другие, составим неравество и решим его.
g₁+g₂+g₃>g₄+g₅ ⇒ x+(x+1)+(x+2)>(x+3)+(x+4)
3x+3>2x+7; 3x-2x>7-3; x>4, 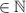 ⇒ x=5
⇒ x=5
Получаем, что минимальный суммарный вес для всех гирь 5+(5+1)+(5+3)+(5+4)+(5+5) = 5+6+7+8+9 = 35.
ответ: 35 грамм.
Р=0,16*0,8+0,4*0,9+0,44*0,7=0,796
3. По формуле Байеса
Р=0,44*0,7/0,796=0,387
2 вероятность дефектной детали р=8/24=1/3
По формуле Бернулли находим
Р(3)=
1. n=4 p=0.24 q=1-p=0.76 m=0,1,2,3,4
по формуле Бернулли находим
Р(0)=
P(1)=
P(2)=
P(3)=
P(4)=
X 0 1 2 3 4
P 0.3336 0.4214 0.1996 0.042 0.0034