
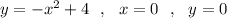
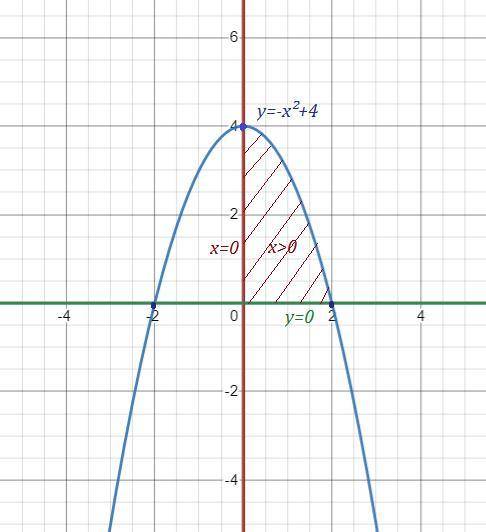
Если задано х=0, то непонятно, площадь какой области находить, слева или справа от прямой х=0. Если задано х>0 , то тогда это правая область, если х<0 , то тогда это левая область . Если вообще не было бы написано уравнение х=0, то эта область находится под параболой до оси ОХ (у=0) .
Найдём площадь правой области при условии х>0 . Если нужна площадь левой области, то она такая же, как и площадь правой области в силу симметрии криволинейной трапеции . Если нужна площадь всей области между параболой и осью ОХ , то она равна удвоенной площади правой области .
Точки пересечения:
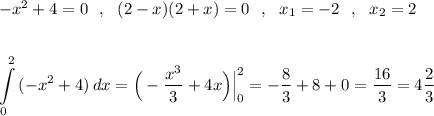
Объяснение:
{ sin(x)+cos(y)=0 ,
{ cos(2x)-cos(2y)=1 ;
{ cosy = - sinx ,
{ cos2x = 1 + cos2y ;
{ cosy = - sinx ,
{ cos²x - sin²x = 2cos²y ;
{ cosy = - sinx ,
{ cos²x - sin²x = 2sin²x ; рішаємо ІІ рівняння :
1 - sin²x - sin²x = 2sin²x ;
4sin²x = 1 ;
sin²x =1/4 ;
a ) sinx = - 1/2 ; або б ) sinx = 1/2 ;
x₁ = ( - 1 )ⁿ⁺¹ π/6 + πn, nЄ Z ; x₂ = ( - 1 )ⁿ π/6 + πn , nЄ Z ;
cosy = - ( - 1/2) = 1/2 ; cosy = 1/2 ;
y₁ = ± π/3 + 2πm , mЄ Z ; y₂= ± 2π/3 + 2πm , mЄ Z .