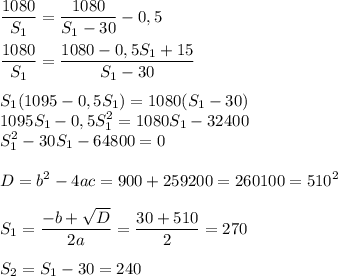
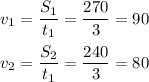
Обозначим числа x1, x2, x3, x4, разность арифметической прогрессии -d (минус, потому что она убывающая), тогда x2=x1-d, x3=x1-2d.
Причём d > 0
Знаменатель геометрической прогрессии обозначим q.
x3=x1-2d=x2*q=(x1-d)*q
x4=x2*q^2=(x1-d)*q^2
x1+x4=x1+(x1-d)*q^2=7
x2+x3=x1-d+x1-2d=6
Из 4 уравнения
x1=(6+3d)/2=3+1,5d
x2=a1-d=3+0,5d
x3=a2-d=3-0,5d=(3+0,5d)*q
q=(3-0,5d)/(3+0,5d)
q^2=(3-0,5d)^2/(3+0.5d)^2
x1+x4=3+1,5d+(3+0,5d)(3-0,5d)^2/(3+0,5d)^2=7
3+1,5d+(3-0,5d)^2/(3+0,5d)=7
Умножаем на знаменатель.
(3+1,5d)(3+0,5d)+(3-0,5d)^2=7(3+0,5d)
9+4,5d+1,5d+0,75d^2+9-3d+0,25d^2=21+3,5d
18+3d+d^2-21-3,5d=0
d^2-0,5d-3=0
2d^2-d-6=0
D=1-4*2(-6)=49=7^2
d1=(1-7)/4=-6/4<0 -не подходит
d2=(1+7)/4=2>0 - подходит.
d=2; x1=3+1,5d=3+3=6;
x2=6-2=4; x3=4-2=2;
q=x3/x2=2/4=0,5; x4=2*0,5=1.
ответ: 6; 4; 2; 1
Есть такая формула для синуса, называется синус двойного угла.
Sin(2a)=2 sin(a) * cos(a), в данном случае она как раз есть в числителе. Сокращаем числитель по этой формуле.Также нужно не забыть поделить 36 на 2, так как только благодаря умножению на 2 получается данное число. Получаем 18sin(102*2)/sin(204)=18sin(204)/sin(204)=18
2)50sin(179)*cos(179)/ sin(358)
Аналогичное задание.
Sin(2a)=2 sin(a)*cos(a)
25 sin(358)/sin(358) = 25
3)42sin(28)*cos(28) / sin(56)
Опять та формула, получаем
21 sin(56) / sin(56) = 21
4)44sin(53)*cos(53) / sin (106)
22 sin(106)/sin(106) = 22
Как видишь ничего трудного, все задания аналогичны и решаются с одной формулы.