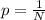, N - общее кол-во шариков.
.
;
;
.
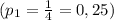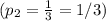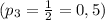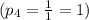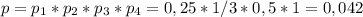
Биномиальное распределение стремится к нормальному при больших n
По условию
р = 0.9
соответственно
q = 1- p = 0.1
Математическое ожидание
М= np= 1000 * 0.9 = 900
Дисперсия
D= npq = 1000*0.9*0.1= 90
Сигма = √D= 3√10 = ~9.5
Мы рассматриваем интервал от центра распределения 900 до 940 - это больше чем четыре сигмы.
В этом случае в табличку нормального распределения можно даже не заглядывать, хвостик за четыремя сигмами очень малюсенький, пятый знак после запятой.
Половина всей выборки до 900 , половина после.
ответ
Вероятность равна ~0.5
315/(18+х)+315/(18-х)+4=40
315/(18+х)+315/(18-x)=36 I÷9
35/(18+x)+35/(18-x)=4
630-35x+630+35x=4(18²-x²)
4x²=1296-1260
4x²=36
x²=9
x₁=3 x₂=-3 x₂∉
x=3 (км/ч).