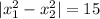 тогда и только тогда, когда
тогда и только тогда, когда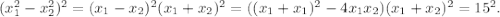 Обозначим через t сумму корней. По т. Виета
Обозначим через t сумму корней. По т. Виета 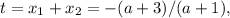
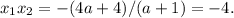 Таким образом,
Таким образом, 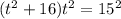 . Отсюда
. Отсюда 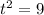 и
и 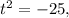 т.е.
т.е. 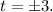 Значит, из условия
Значит, из условия 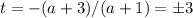 находим a=-3/2 и a=0. В обоих случаях дискриминант уравнения положителен, т.е. имеются 2 действительных корня, поэтому ответ a=-3/2 и a=0.
находим a=-3/2 и a=0. В обоих случаях дискриминант уравнения положителен, т.е. имеются 2 действительных корня, поэтому ответ a=-3/2 и a=0.