Объяснение:
1 . ( x² - x )/3 = ( 2x + 4 )/5 ; │X 15 2 . ( 2x² + x )/5 = ( 4x - 2 )/3 ;│X 15
5( x² - x ) = 3( 2x + 4 ) ; 3( 2x² + x ) = 5( 4x - 2 ) ;
5x² - 5x = 6x + 12 ; 6x² + 3x = 20x - 10 ;
5x² - 5x - 6x - 12 = 0 ; 6x² + 3x - 20x + 10 = 0 ;
5x² - 11x - 12 = 0 ; 6x² - 17x + 10 = 0 ;
D = 361 > 0 ; x₁ = - 0,8 ; x₂ = 3 . D = 49 > 0 ; x₁ = 5/6 ; x₂ = 12/13 .
3 . ( x² - x )/2 = 5 + 6x ;│X 2
x² - x = 10 + 12x ;
x² - x - 12x - 10 = 0 ;
x² - 13x - 10 = 0 ; D = 209 > 0 ; x₁= (13 - √209 )/2 ; x₂ = (13 - √209 )/2 .


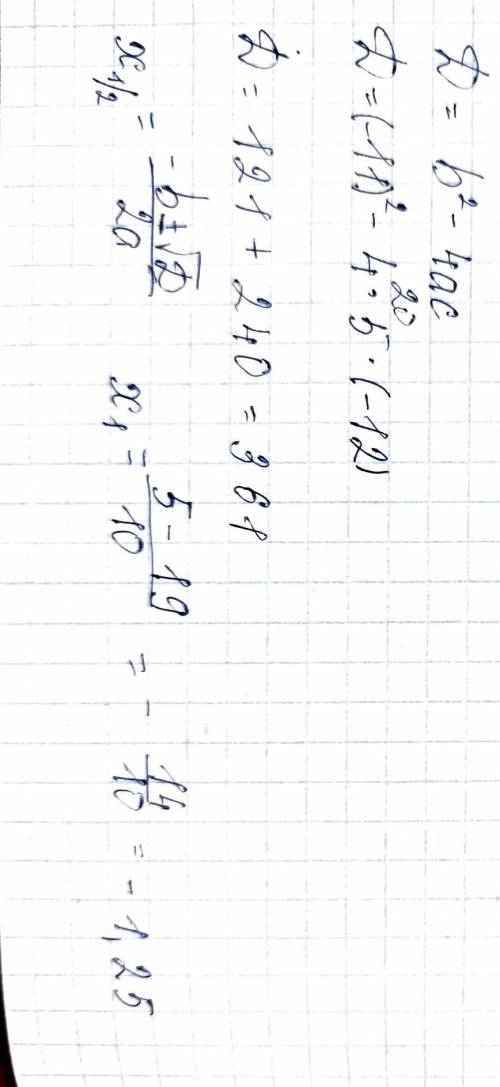
вот прочитай теорию
Линейная функция — это функция, которую можно задать формулой
y=kx+m , где x — независимая переменная, k и m — некоторые числа.
Применяя эту формулу, зная конкретное значение x , можно вычислить соответствующее значение y .
Пусть y=0,5x−2 .
Тогда:
если x=0 , то y=−2 ;
если x=2 , то y=−1 ;
если x=4 , то y=0 и т. д.
Обычно эти результаты оформляют в виде таблицы:
x 0 2 4
y −2 −1 0
x — независимая переменная (или аргумент),
y — зависимая переменная.
Графиком линейной функции y=kx+m является прямая.
Чтобы построить график данной функции, нам нужны координаты двух точек, принадлежащих графику функции.
Построим на координатной плоскости xOy точки (0;−2) и (4;0) и
проведём через них прямую.
lineara1.png
Многие реальные ситуации описываются математическими моделями, представляющими собой линейные функции.
Пример:
на складе было 500 т угля. Ежедневно стали подвозить по 30 т угля. Сколько угля будет на складе через 2 ; 4 ; 10 дней?
Если пройдёт x дней, то количество y угля на складе (в тоннах) выразится формулой y=500+30x .
Таким образом, линейная функция y=30x+500 есть математическая модель ситуации.
При x=2 имеем y=560 ;
при x=4 имеем y=620 ;
при x=10 имеем y=800 и т. д.
Однако надо учитывать, что в этой ситуации x∈N .
Если линейную функцию y=kx+m надо рассматривать не при всех значениях x , а лишь для значений x из некоторого числового множества X , то пишут y=kx+m,x∈X .
Пример:
построить график линейной функции:
a) y=−2x+1,x∈[−3;2] ; b) y=−2x+1,x∈(−3;2) .
Составим таблицу значений функции:
x −3 2
y 7 −3
Построим на координатной плоскости xOy точки (−3;7) и (2;−3) и
проведём через них прямую.
Далее выделим отрезок, соединяющий построенные точки.
Этот отрезок и есть график линейной функции y=−2x+1,x∈[−3;2] .
Точки (−3 ; 7) и (2 ; −3) на рисунке отмечены тёмными кружочками.
lineara2.png
b) Во втором случае функция та же, только значения x=−3 и x=2 не рассматриваются, так как они не принадлежат интервалу (−3;2) .
Поэтому точки (−3 ; 7) и (2 ; −3) на рисунке отмечены светлыми кружочками.
lineara3.png
Рассматривая график линейной функции на отрезке, можно назвать наибольшее и наименьшее значения линейной функции.
В случае
a) y=−2x+1,x∈[−3;2] имеем, что yнаиб =7 и yнаим =−3 ;
b) y=−2x+1,x∈(−3;2) имеем, что ни наибольшего, ни наименьшего значений линейной функции нет, так как оба конца отрезка, в которых как раз и достигались наибольшее и наименьшее значения, исключены из рассмотрения.
В ходе построения графиков линейных функций можно как бы «подниматься в горку» или «спускаться с горки», т. е. линейная функция или возрастает, или убывает.
Если k>0 , то линейная функция y=kx+m возрастает;
если k<0 , то линейная функция y=kx+m убывает.
Объяснение:
6+3+6=15
3:15=0,2
0,2=20%