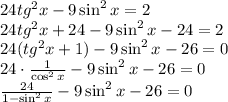
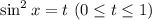 , тогда получаем
, тогда получаем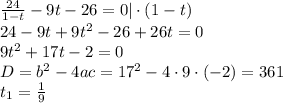
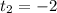 - не удовлетворяет условию при
- не удовлетворяет условию при ![t \in [0;1].](/tpl/images/0409/3253/664ce.png)
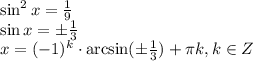
S = 64 см²
Объяснение:
r = 4 см
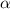 = 30
= 30
S - ?
=============
Должно выполняться условие, что суммы противоположных сторон четырехугольника равны - только тогда получиться вписать в него окружность.
Распишем это условие:  ⇔
⇔ 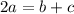 . где a - боковые стороны, b и c - основы.
. где a - боковые стороны, b и c - основы.
Сделаем вывод, что трапеция являеться равнобедренной.
Формула для нахождения площади через среднюю линию и высоту трапеции: 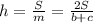 ⇔
⇔  , где S - площадь трапеции, m - средняя линия трапеции, h - ее высота.
, где S - площадь трапеции, m - средняя линия трапеции, h - ее высота.  , b и c - основы трапеции.
, b и c - основы трапеции.
Зная радиус вписаной окружности, мы знаем высоту трапеции:  ⇔
⇔  .
.
Соответственно, из прямоугольного треугольника ADH1 найдём боковую сторону трапеции с соотношений: 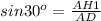 ⇒
⇒  см - боковая сторона трапеции.
см - боковая сторона трапеции.
Если  , то зная а = 8, можем найти среднюю линию, а соответственно и площадь.
, то зная а = 8, можем найти среднюю линию, а соответственно и площадь. 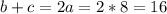 см.
см.
Просто подставляем в формулу площади: 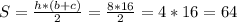 см².
см².

24tg^2 x + 24 - 24 - 9sin^2 x - 2 = 0
24(1 + tg^2 x) - 9(1 - cos^2 x) - 26 = 0
24*1/cos^2 x + 9cos^2 x - 9 - 26 = 0
Замена cos^2 x = y, по определению косинуса 0 <= y <= 1
24/y + 9y - 35 = 0
9y^2 - 35y + 24 = 0
D = 35^2 - 4*9*24 = 1225 - 864 = 361 = 19^2
y1 = cos^2 x = (35 - 19)/18 = 16/18 = 8/9
y2 = cos^2 x = (35 + 19)/18 = 54/18 = 3 > 1 - не подходит
cos^2 x = 8/9
1) cos x = -2√2/3; x1 = +- arccos (-2√2/3) + 2pi*k
2) cos x = 2√2/3; x2 = +- arccos (2√2/3) + 2pi*n
Если cos^2 x = 8/9, то sin^2 x = 1/9; sin x = +-1/3
Так что мы оба получили одинаковые ответы.