Найти все значения а, при которых неравенство (х+3-2а)(х+3а-2)< 0 выполняется для всех х, таких, что 2< =x< =3

👇

Ответ:

alena0bashinskaya

19.03.2023

(x + 3 - 2a)(x + 3a - 2) < 0
(x - (2a - 3))(x - (2 - 3a)) < 0
1) Пусть 2a - 3 < 2 - 3a; то есть 5a < 5; a < 1; тогда
2a - 3 < x < 2 - 3a
По условию 2 <= x <= 3, значит
{ 2a - 3 < 2
{ 2 - 3a > 3
Отсюда
{ 2a < 5; a < 5/2
{ 3a < -1; a < -1/3 < 1
Значит a < -1/3

2) Пусть 2a - 3 > 2 - 3a; то есть a > 1; тогда
2 - 3a < x < 2a - 3
По условию 2 <= x <= 3, значит
{ 2 - 3a < 2
{ 2a - 3 > 3
Отсюда
{ -3a < 0; a > 0
{ 2a > 6; a > 3 > 1
Значит a > 3
ответ: a принадлежит (-oo; -1/3) U (3; +oo)

4,8(56 оценок)

Открыть все ответы

Ответ:

IrynadiV

19.03.2023

2) D(y)=(-∞; -6]∪[1; +∞)

3)Смотреть изображение

4)-9; 3

Объяснение:

2) Область определения ф-ции - все значения, которые может принимать независимая переменная (х). Подкоренное выражение корня чётной степени должно быть не меньше нуля, поэтому чтобы найти область определения нужно решить неравенство

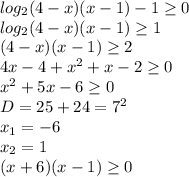
$log_2(4-x)(x-1)-1\geq 0\\log_2(4-x)(x-1)\geq 1\\(4-x)(x-1)\geq 2\\4x-4+x^2+x-2\geq 0\\x^2+5x-6\geq 0\\D=25+24=7^2\\x_1=-6\\x_2=1\\(x+6)(x-1)\geq 0$

x∈(-∞; -6]∪[1; +∞)

Тогда D(y)=(-∞; -6]∪[1; +∞)

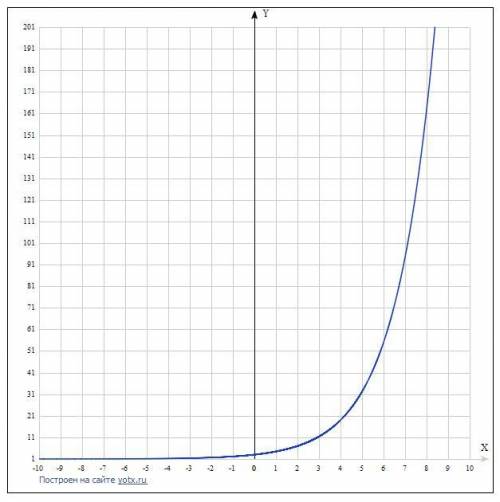
3) Чтобы построить график функции нужно построить график обычной показательной функции без второстепенных коэффициентов. Берём любые значения икса и считаем чему при данных значениях будет равен игрек. Точки с полученными координатами выставляем на координатную плоскость и проводим через эти точки график функции. Потом смещаем график в соответствии с коэффициентами. Свободные коэффициенты указывают на сколько клеток нужно сместить график по ординате. Коэффициент перед иксом Сжимает график по абсциссе обратить внимание, что данная функция является показательной и абсцисса здесь будет являться асимптотой, и график её никогда не пересечёт, хотя будет всё больше и больше приближаться к ней.

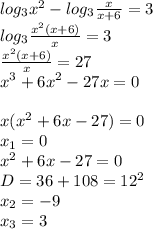
$log_3x^2-log_3\frac{x}{x+6} =3\\log_3\frac{x^2(x+6)}{x} =3\\\frac{x^2(x+6)}{x} =27\\x^3+6x^2-27x=0\\\\x(x^2+6x-27)=0\\x_1=0\\x^2+6x-27=0\\D=36+108=12^2\\x_2=-9\\x_3=3$

Не забываем про ОДЗ

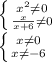
$\left \{ {{x^2\neq 0} \atop {\frac{x}{x+6}\neq 0 }} \right. \\\left \{ {{x\neq 0} \atop {x\neq -6}} \right.$

С учётом ОДЗ корень 0 не является корнем уравнения. В ответ идут только -9 и 3

4,5(79 оценок)

Ответ:

maryamromanenko1294

19.03.2023

Сразу скажем, что в таком виде результат неверен, более того, сумму квадратов обратных величин можно сделать сколь угодно близкой к нулю. Например, 104-100+100-100=4, а 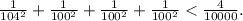$\frac{1}{104^2}+\frac{1}{100^2}+\frac{1}{100^2}+\frac{1}{100^2}$

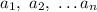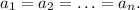
А вот если все четыре числа положительны, требуемое неравенство легко выводится из неравенства Коши между средним арифметическим и средним геометрическим: для неотрицательных $a_1,\ a_2,\ \ldots a_n$ справедливо неравенство $\frac{a_1+a_2+\ldots +a_n}{n}\ge \sqrt[n]{a_1\cdot a_2\cdot \ldots \cdot a_n},$ причем неравенство превращается в равенство только в случае $a_1=a_2=\ldots =a_n.$

Из условия a+b+c+d=4 и неравенства Коши (если a, b, c, d положительны) следует, что $1=\frac {a+b+c+d}{4}\ge \sqrt[4]{a\cdot b\cdot c\cdot d}.$ Иными словами,