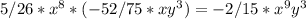
1. x2 - 9x + 20 = 0
По теореме Виетта
x1 + x2 = 9
x1 × x2 = 20
(То есть нам нужно найти 2 таких числа, при сложении которых получилось бы 9, а при умножении 20)
х1 = 4
х2 = 5
2. х2 - 6х + 8
а) (a - b)2
x2 - 2x × 3 + 8
x2 - 2x × 3 + 9 - 9 + 8
x2 - 2x × 3 + 9 - 9 + 8 = (x - 3)2 - 1
б) представим выражение в виде
х2 - 2х - 4х + 8 (для того, чтобы мы могли потом использовать группировки). теперь вынесем общий множитель у пар
х(х - 2) - 4(х - 2)
теперь снова вынесем общий множитель (в данном случае это целая скобка)
(х - 2)(х - 4)
В круглых скобках - НОД чисел. Ищем алгоритмом Евклида
7) (75, 45) = (45, 30) = (15, 30) = 15
8) (20, 35) = (20, 15) = (5, 15) = 5
9) (80, 64) = (64, 16) = 16
10) (240, 210) = (30, 210) = 30
11) (396, 180 ) = (36, 180) = 36
12) (1001, 186) = (186, 71) = (71, 44) = (44, 27) = (27, 17) = (10, 17) = (7, 10) = (3, 7) = (1, 3) = 1
13) (60, 45) = (15, 45) = 15
14) (63, 105) = (63, 42) = (42, 21) = 21
15) (120, 96) = (96, 24) = 24
16) (170, 102) = (102, 68) = (34, 68) = 34
17) (210, 350) = (140, 210) = (140, 70) = 70
18) (1225, 1800) = (1225, 575) = (575, 75) = (50, 75) = (75, 25) = 25