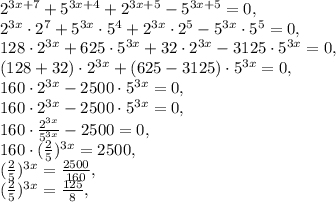
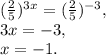
Так как в уравнении есть квадратные корни, то запишем ОДЗ:
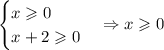
Также заметим, что в левой части записано произведение двух неотрицательных выражений. Значит, правая часть уравнения также неотрицательна:
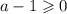
Таким образом, при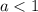 
уравнение не имеет корней.
Предположим, что . Тогда:
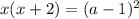
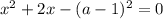
Проверим, удовлетворяют ли найденные корни ОДЗ.
Для первого корня получим:
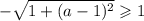
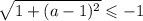
Однако, квадратный корень не может принимать отрицательных значений. Значит, рассматриваемое выражение не является корнем уравнения ни при каких значениях параметра 
.
Для второго корня получим:
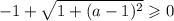
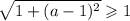
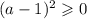
Последнее условие выполняется при любых значениях параметра . Но как отмечалось ранее, уравнение может иметь корни только при . Значит, данное выражение является корнем уравнения при .
при 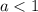: нет корней,
при : 
Объяснение:
рассмотрим параллельный ряд тонких полос на расстоянии D > d друг от друга
монета размером d попадет внутрь и не заденет полосы с вероятностью (D-d)/D
второй ряд перпендикулярен первому
имеет тот-же размер
монета размером d попадет внутрь второго ряда и не заденет полосы с вероятностью (D-d)/D
так как ряды перпендикулярны то события попадания и непопадания на полосы одного и другого ряда независимы
значит вероятность монеты размером d не пересечь ни одной из сторон квадрата размером D является произведением двух вероятностей
( (D-d)/D ) ^2 = 0,4
( (D-d)/D ) = корень(0,4)
1 - d/D = корень(0,4)
1 - корень(0,4) = d/D
D = d/(1 - корень(0,4) ) ~ 2,7 * d
ответ D ~ 2,7 * d
