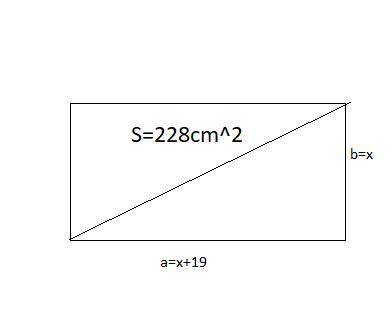
Объяснение:
диагоналей прямоугольника: d=?
ширина прямоугольника a=x
длина прямоугольника:b=x+19
S=a*b
228=x(x+19)
228=x²+19x
X²+19x=228
X²+19x-228=0
Δ=361+912=1273
√Δ=√1273=35,7
X1=(-19-35,7)/2=-54,4 длина не может быть отрицательной
X2=(-19+35,7)/2=16,7/2=8,35
ширина прямоугольника a=x=8,35cm
длина прямоугольника:b=x+19=8,35+19=27,35cm
диагоналей прямоугольника: из формулы d²==a²+b²
d²= 27,35²+8,35²=748+70=818
d=√818=28,6cm
OTBET: диагоналей прямоугольника d=28,6cm
выразим y:
x^(1/2)+y^(1/2)=a^(1/2)
y^(1/2) = a^(1/2) - x^(1/2)
y = [a^(1/2) - x^(1/2)]^2 = a + x - 2(ax)^(1/2);
x+y=a
y = a - x
Найдем точки пересечения этих функций, приравняв их:
a + x - 2(ax)^(1/2) = a - x
2x = 2(ax)^(1/2)
x = (ax)^(1/2)
x^2 = ax
x^2 - ax = 0
x(x - a) =
x = 0 и x = a точки пересечения
Площадь фигуры - это интеграл, где точки пересечения - это пределы интегрирования