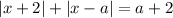
Найдем нули подмодульных выражений:
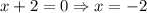
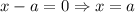
Возможны две ситуации взаимного расположения этих точек: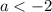 
и 
.
Заметим, что первая ситуация не дает решений, так как при 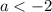выражение в правой части уравнения 
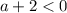, но с другой стороны это выражение есть сумма модулей, которая не может быть отрицательной. Значит, при 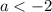уравнение не имеет решений.
Рассмотрим ситуацию . Раскроем модуль при трех условиях:
1. Пусть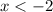 
. Тогда оба модуля раскрываются со сменой знака:
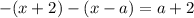
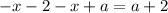
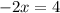
Но по условию раскрытия модулей 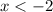. Значит, в данном случае корней нет.
2. Пусть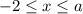 
. Тогда первый модуль раскрывается без смены знака, а второй - со сменой знака:
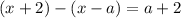
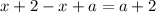
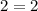
Это верное равенство. Значит, решениями являются все значения, при которых было сделано такое раскрытие модулей:
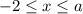
3. Пусть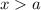 
. Тогда оба модуля раскрываются без смены знака:
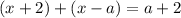
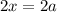
Но по условию раскрытия модулей 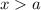. Значит, в данном случае корней нет.
Таким образом, корни имеются только при условии . Они определяются соотношением .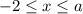
Выделив условие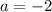 
как частный случай, можно записать ответ.
при 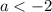: нет корней
при 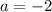: один корень
при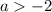 
: бесконечное множество корней: ![x\in[-2;\ a]](/tpl/images/1359/9802/14c1d.png)
Всё очень просто там а · в = а - 5в
Под величиной В дан пример 2Δ(3 · 4 )
а · в =3 · 4
Подставляешь
3 · 4 = 3-5·4 = -17
В примере аΔв= в+2а то же самое
Под величиной А пример 3 ·(5Δ4), они совпадают
Подставляешь
5Δ4= 4+2·5=14
А теперь смотришь что получается
Под примером А = 3·14
Под примером В = 2Δ(-17)
И то же самое по формулам:
а · в = а - 5в
аΔв= в+2а
Считаем пример А- а · в = 3·14 = 3-5·14 = - 67
Считаем пример В - аΔв=2Δ(-17) = (-17) + 2·2= -13
Вот вам и окончательные ответы
А = - 67
В = -13
Теперь посмотрим на твои варианты ответов
А · В = (- 67) · (-13)= 871
Число больше нуля, оно не подходит
А + В = (- 67) + (-13)= (-80)
Число меньше нуля, оно не подходит
Объяснение:
Подставляйте А = - 67 и В = -13 в формулы и считайте какой вариант подходит, а какой нет
x³(3+x²)+3³(x²+3)=(x³+3³)(x²+3)=0=(x+3)(x²-3x+9)(x²+3)=0
x=-3
x²+3, x²-3x+9 корней не имеют D<0