Question

Обратите число в обыкновенную дробь: 1)0,2(3); 2)1,(81); 3)0,32(45); 4) 1,6(3201)"

Answer 1

1).

$\displaystyle 0,2(3)=0,2+0,0(3)=\frac{2}{10} +\frac{3}{90} = \frac{18+3}{90}= \frac{21}{90} = \boxed {\frac{7}{30} }$

2).

$\displaystyle 1,(81)=1+\frac{81}{99} = 1+\frac{9}{11} = \boxed{1\frac{9}{11}}$

3).

$\displaystyle 0,32(45)=0,32+0,00(45)=\frac{32}{100} +\frac{45}{9900} = \frac{3168+45}{9900} = \frac{3213}{9900} = \boxed{\frac{357}{1100}}$

4).

$\displaystyle 1,6(3201)=1+0,6+0,0(3201)=1+\frac{6}{10} +\frac{3201}{99990} = {1} \frac{59994+3201}{99990} = \\= 1\frac{63195}{99990} = \boxed{1\frac{383}{606}}$

Answer 2

Приведу другой через геометрическую прогрессию)

$0{,}2(3)=0{,}2+0{,}03+0{,}003+0{,}0003+...~\boxed{=}$

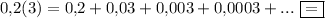
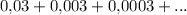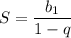
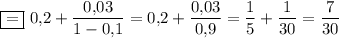
Сумма $0{,}03+0{,}003+0{,}0003+...$ это сумма бесконечно убывающей геометрической прогрессии. Сумма бесконечно убывающей геометрической прогрессии вычисляется по формуле $S=\dfrac{b_1}{1-q}$

$\boxed{=}~0{,}2+\dfrac{0{,}03}{1-0{,}1}=0{,}2+\dfrac{0{,}03}{0{,}9}=\dfrac{1}{5}+\dfrac{1}{30}=\dfrac{7}{30}$

ответ: 7/30.

$1{,}(81)=1+0{,}81+0{,}0081+0{,}000081+...~\boxed{=}$

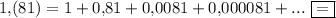
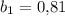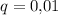
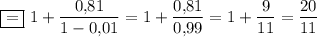
Бесконечно убывающая геометрическая прогрессия с первым членом $b_1=0{,}81$ и знаменателем $q=0{,}01$

$\boxed{=}~ 1+\dfrac{0{,}81}{1-0{,}01}=1+\dfrac{0{,}81}{0{,}99}=1+\dfrac{9}{11}=\dfrac{20}{11}$

ответ: 20/11.

$0{,}32(45)=0{,}32+0{,}0045+0{,}000045+0{,}00000045+...~\boxed{=}$

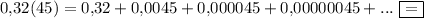
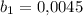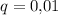
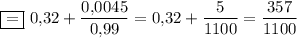
Имеем бесконечно убывающую геометрическому прогрессию с первым членом $b_1=0{,}0045$ и знаменателем $q=0{,}01$

$\boxed{=}~ 0{,}32+\dfrac{0{,}0045}{0{,}99}=0{,}32+\dfrac{5}{1100}=\dfrac{357}{1100}$

ответ: 357/1100.

$1{,}6(3201)=1{,}6+0{,}03201+0{,}000003201+...~\boxed{=}$

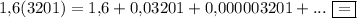
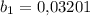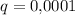
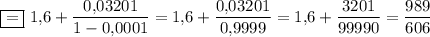
Видим сумму бесконечно убывающей геометрической прогрессии с первым членом $b_1=0{,}03201$ и знаменателем $q=0{,}0001$

$\boxed{=}~1{,}6+\dfrac{0{,}03201}{1-0{,}0001}=1{,}6+\dfrac{0{,}03201}{0{,}9999}=1{,}6+\dfrac{3201}{99990}=\dfrac{989}{606}$

ответ: 989/606.