ответ:
x∈(-∞; -6)∪(6; 10]
объяснение:
(x^2-16x+60)/(x^2-36)≤0
y=(x^2-16x+60)/(x^2-36)
(x^2-16x+60)/(x^2-36)=0
1) x^2-16x+60=0
d=256-4*60=256-240=16
2) x^2-36≠0
x^2≠36
x≠6
x≠-6
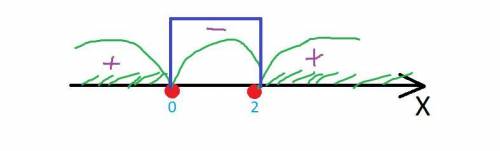
- + - +
---()()*>
(-6) (6) 10
x∈(-∞; -6)∪(6; 10]
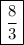 квадратных единиц
квадратных единиц
Объяснение:
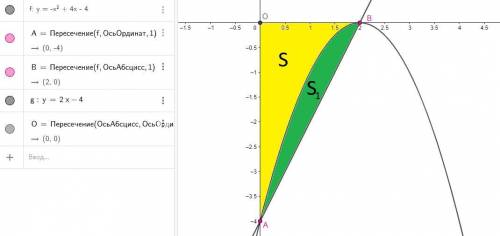
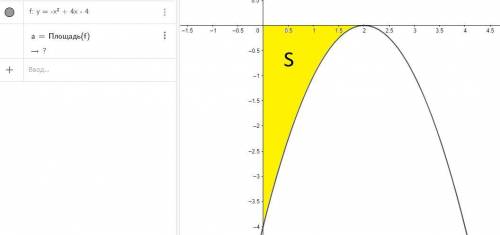
Построим график 
Пусть S площадь ограниченная графиком функции  осями координат. Пусть точка B - пересечение графика y и оси абсцисс, точка A - пересечение графика y и оси ординат.
осями координат. Пусть точка B - пересечение графика y и оси абсцисс, точка A - пересечение графика y и оси ординат.
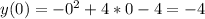
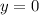
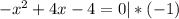
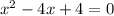

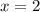
Координаты точек A и B:
A(0;-4)
B(2;0)
Пусть точка начало системы координат, тогда точка O имеет координаты O(0;0).
Узнаем уравнение прямой проходящей через точки A и B. Уравнение прямой с угловым коэффициентом в общем виде:  .
.
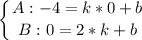
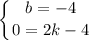
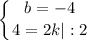
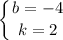
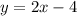
Пусть 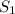 - площадь между прямой
- площадь между прямой 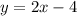 и функцией
и функцией 
Пусть 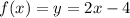 и
и  .
.
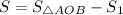
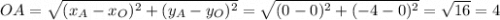
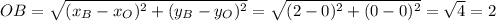
По формуле площади прямоугольного треугольника:
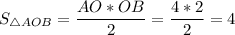 .
.
Промежуток интегрирования: ![[0;2]](/tpl/images/4566/3708/2ae13.png)
Докажем, что  при
при ![x \in [0;2]](/tpl/images/4566/3708/4a92d.png)

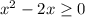

![x \in (-\infty;0] \cup [2;+\infty)](/tpl/images/4566/3708/254e2.png) тогда можно сделать вывод, что
тогда можно сделать вывод, что
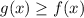 при
при ![x \in [0;2]](/tpl/images/4566/3708/4a92d.png) .
.
По теореме:

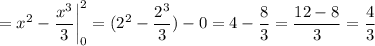 .
.
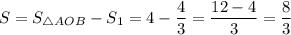 квадратных единиц.
квадратных единиц.
Во первых число, которое дано в задании является радианной мерой угла.
Если начинать отсчет против часовой стрелки (угол положителен), и повернуть на 180 градусов (полуокружность), то в радианах это будет
Найдем приблизительно, сколько радиан в 90 градусах:
Следовательно при повороте на
Значит, 4 радиана находиться где то между
2)
Найдем количество оборотов на 90 градусов для числа 8:
Т.е. мы делаем полный оборот (он равен приблизительно 4 оборотам на 90 градусов) + один оборот на 90 градусов + оборот на 0.3 радиана.
Следовательно 8 находиться в 2 четверти.
3)
Здесь мы делаем обороты по часовой стрелке (угол отрицателен).
Снова находим количество оборотов :
Это 1 полный оборот, + оборот на 180 градусов.
То есть, -9 радиан находится где то на 3 четверти.
4)
Приблизительно 5,15 полных оборотов. Т.е. 5 полных оборотов + оборот на 0.15 радиан.
Т.е. 31 находится где то на 1 четверти.