Пусть  при этом
при этом  , получим квадратное уравнение относительно t
, получим квадратное уравнение относительно t
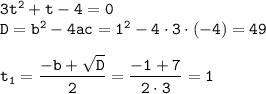
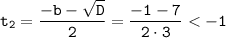 - не удовлетворяет условию
- не удовлетворяет условию
Обратная замена:
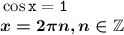
Отбор корней на промежутке [0;π].
Если 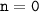 , то
, то 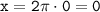
sin⁴(π/16) + sin⁴(3π/16) + sin⁴(5π/16) + sin⁴(7π/16) = (1 - cos(π/8))²/4 +
+ (1 - cos(3π/8))²/4 + (1 - cos(5π/8))²/4 + (1 - cos(7π/8))²/4 = (1/4) •
• ( 1 - 2cos(π/8) + cos²(π/8) + 1 - 2cos(3π/8) + cos²(3π/8) + 1 - 2cos(5π/8) + cos²(5π/8) + 1 - 2cos(7π/8) + cos²(7π/8) ) = (1/4) • ( 4 - 2•( cos(π/8) + cos(3π/8) + cos(5π/8) + cos(7π/8) ) + ( cos²(π/8) + cos²(3π/8) + cos²(5π/8) + cos²(7π/8) ) ) = (1/4) • ( 4 - 2•( 2•cos(π/2)•cos(-3π/8) + 2•cos(π/2)•cos(-π/8) ) + ( cos²(π/8) + cos²(3π/8) + cos²(5π/8) + cos²(7π/8) ) ) = 1 + (1/4)•( cos²(π/8) + cos²(3π/8) + cos²(5π/8) + cos²(7π/8) ) = 1 + (1/4)•( ( cos(π/8) + cos(7π/8) )² + ( cos(3π/8) + cos(5π/8) )² - 2•cos(π/8)•cos(7π/8) - 2•cos(3π/8)•cos(5π/8) ) =
= 1 - (1/4)•( cosπ + cos(-3π/4) + cosπ + cos(-π/4) ) = 1 - (1/4)•( - 2 - (√2/2) + (√2/2) ) = 1 - (1/4)•(-2) = 1 + 0,5 = 1,5
ответ: 1,5
Данное уравнение сводится к квадратному уравнению, поэтому сделаем замену:
Пусть cosx = t , но | t | ≤ 1
D = b² - 4ac = 1² - 4 × 3 × ( - 4 ) = 1 + 48 = 49 = 7²
t = ( - 1 ± 7 ) / 6
1) t = - 4 / 3 - не подходит по условию | t | ≤ 1
2) t = 1 - подходит
Обратная замена:
n принадлежит Z
На промежутке [ 0 ; π ] подходит только х = 0
ОТВЕТ: 0