Часовая стрелка проходит 5 делений циферблата в час, минутная - 60 делений.
За минуту часовая проходит 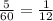 часть деления, минутная - 1 деление. Значит за 1 минуту минутная стрелка "догоняет" часовую на
часть деления, минутная - 1 деление. Значит за 1 минуту минутная стрелка "догоняет" часовую на 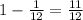 часть деления.
часть деления.
В настоящий момент стрелки разделяет 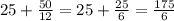 деления (см. рис. - считаем по часовой стрелке).
деления (см. рис. - считаем по часовой стрелке).
Когда минутная стрелка в первый раз поравняется с часовой, ей нужно будет "догнать" часовую ещё 7 раз, сократив расстояние на 60 делений, то есть всего на 60·7 = 420 делений.
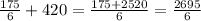 делений нужно пройти минутной стрелке, чтобы в восьмой раз поравняться с часовой.
делений нужно пройти минутной стрелке, чтобы в восьмой раз поравняться с часовой.
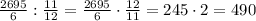 минут понадобится, чтобы минутная стрелка в восьмой раз поравнялась с часовой
минут понадобится, чтобы минутная стрелка в восьмой раз поравнялась с часовой

3√3 > 5
Объяснение:
Эти числа можно по разному сравнивать, самый легкий поднести обе части до квадрата, сделать соответствующие арифметические операции, и увидеть - какое число больше.
Птичка ^ обозначает, что сейчас эти числа сравниваются:
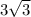 ^ 5;
^ 5;
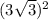 ^ 5²;
^ 5²;
 ^ 25
^ 25
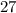 ^ 25- Что больше? Разумеется 27, значит 3√3 больше 5. То есть, 3√3 > 5.
^ 25- Что больше? Разумеется 27, значит 3√3 больше 5. То есть, 3√3 > 5.
Просто взять и узнать приближенное значение √3 = 1,73. Узнав, просто взять 3 * 1,73 = 5,19. А число 5,19 больше за 5, вот и оказывается опять, что 3√3 > 5.
Если вы представите все числа, которые даны в сравнение, как корни этих же чисел, то число будет больше то, под корнем число которое больше. Например, √25 = 5, а √27 = 3√3. Вопрос: что больше, √27 или √25 ? Ну разумеется что √27. Поэтому, 3√3 > 5
Sin²x + Cos²y = 1/2 ⇒ Cos² y + Cos²y = 1/2⇒2Cos²y = 1/2⇒Cos²y = 1/4⇒
⇒Cos y = +-1/√4
а) Cosy = 1/√4 x = +-arcCos1/√4 + 2πk, k ∈Z
Sin x = -1/√4 y = (-1)^n arcSin(-1/√4) + nπ, n∈Z
б)Cosy = -1/√4 x = +-arcCos(-1/√4) + 2πk, k ∈Z
Sin x = 1/√4 y = (-1)^n arcSin1/√4 + nπ, n∈Z