
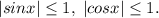
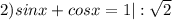
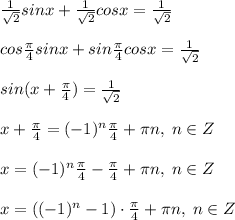
Объяснение:
1) |4-x|<6
__x<4__x=4__x>4__
+ 0 - 4-x
x<4
4-x<6⇒-x<6-4⇒-x<2⇒x>-2 x∈(-2;4]
x>4
-(4-x)<6⇒-4+x<6⇒x<6+4⇒x<10 x∈(4;10)
x∈(-2;10) целых решений : -1,0,1,2,3,4,5,6,7,8,9=11
2) 2|x+3|≤|x-1|⇒2|x+3|-|x-1|≤0
x<-3x=-3-3≤x<1x=1x≥1
- 0 + + x+3
- - 0 + x-1
x<-3
2(-x-3)-(-x+1)≤0⇒-2x-6+x-1≤0⇒-x-7≤0⇒-x≤7⇒x≥-7 x∈[-7;-3)
-3≤x<1
2(x+3)-(-x+1)≤0⇒2x+6+x-1≤0⇒3x≤-5⇒x≤-5/3 x∈[-3;-5/3]
x≥1
2x+6-(x-1)≤0⇒2x+6-x+1≤0⇒x≤-7 x∈∅
x∈[-7;-3)U[-3;-5/3] целых решений: -7,-6,-5,-4,-3,-2=6
1.а) Область определения находим из системы неравенств
х+44>0; 2х-22>0;
х>-44;х>22/2⇒x∈(11;+∞).
4а) ㏒₃(х-4)+㏒₃(х+7)=㏒₃26; ОДЗ уравнения х больше 4, (х-4)(х+7)=26;
х²+7х-4х-28-26=0; х²+3х-54=0; По теореме, обратной теореме Виета, х₁=-9∉ОДЗ, не является корнем. х₂=6
4в) ㏒²₂х-㏒₂х-30=0; ОДЗ уравнения х∈(0;+∞) Пусть ㏒₂х=у, тогда у²-у-30=0; по теореме, обр. теореме Виета, у₁=-5; у₂=6 тогда ㏒₂х=-5; х=2⁻⁵; х=1/32 -входит в ОДЗ, корень.
㏒₂х=6; х=2⁶=64- входит в ОДЗ, корень.
5а)㏒₁/₅(22х-2)≥0
ОДЗ неравенства 22х-2>0; x>1/11
Заменим 0=㏒₁/₅1, т.к. основание логарифма меньше 1, то 22х-2≤1
22х≤3; х≤3/22; с учетом ОДЗ решением неравенства будет х∈(1/11;3/11)